Énoncé
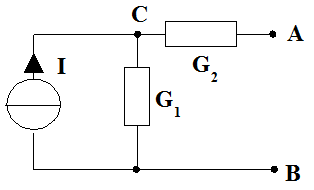
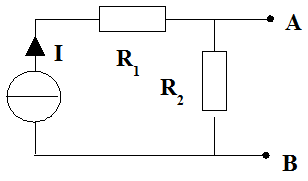
Les deux circuits ci-dessus sont alimentés par des générateurs de courant. Pour chacun d'eux :
1 - En appliquant le théorème de Thévenin, trouver le générateur de tension
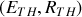 équivalent vu des points
équivalent vu des points
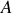 et
et
 .
.
2 - En appliquant le théorème de Norton, trouver le générateur de courant
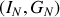 équivalent vu des points
équivalent vu des points
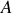 et
et
 .
.
3 - Vérifier à chaque fois que
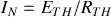 .
.
Pour chaque circuit, calculer
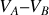 en fonction du courant
en fonction du courant
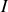 délivré par le générateur, puis la résistance du circuit rendu passif en éteignant la source de courant Ces deux quantités donnent respectivement
délivré par le générateur, puis la résistance du circuit rendu passif en éteignant la source de courant Ces deux quantités donnent respectivement
 et
et
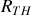 ou
ou
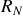 . Calculer ensuite le courant de court-circuit passant de
. Calculer ensuite le courant de court-circuit passant de
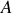 vers
vers
 dans un fil sans résistance. On obtient
dans un fil sans résistance. On obtient
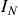 , et on vérifie
, et on vérifie
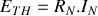 .
.
Rappel de cours :
Réseaux électriques en régime continu : théorème de Thévenin, théorème de Norton.
Les composants électriques dipolaires : générateurs réels, équivalence entre générateur de tension et générateur de courant.
Exercice de référence sur les diviseurs de tension et de courant.
Le calcul de
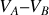 se fait sans problème, en fonction du courant
se fait sans problème, en fonction du courant
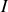 délivré par le générateur, et fournit la fem
délivré par le générateur, et fournit la fem
 du générateur de tension. Se rappeler que
du générateur de tension. Se rappeler que
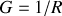 .
.
La résistance
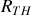 s'obtient en faisant
s'obtient en faisant
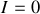 dans chacun des circuits (attention : cela veut dire remplacer le générateur de courant par un interrupteur ouvert, ou encore le supprimer entièrement). La résistance
dans chacun des circuits (attention : cela veut dire remplacer le générateur de courant par un interrupteur ouvert, ou encore le supprimer entièrement). La résistance
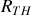 est aussi celle,
est aussi celle,
 , du générateur de Norton.
, du générateur de Norton.
Le courant
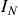 du générateur de Norton s'obtient en reliant
du générateur de Norton s'obtient en reliant
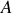 et
et
 par un fil sans résistance. On calcule alors le courant passant dans ce fil (courant de court-circuit).
par un fil sans résistance. On calcule alors le courant passant dans ce fil (courant de court-circuit).
L'équivalence entre les deux générateurs est établie en vérifiant que
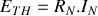 .
.
Circuit 1 :
1 -
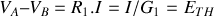 ;
;
 .
.
2 -
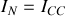 est le courant passant dans
est le courant passant dans
 , soit
, soit
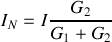 (diviseur de courant) ;
(diviseur de courant) ;
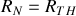 .
.
3 - Vérification immédiate en gardant les expressions de
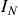 et de
et de
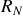 avec les conductances.
avec les conductances.
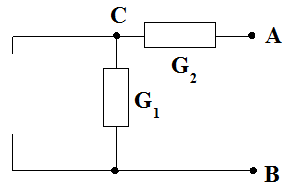
Circuit 2 :
1 –
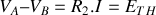 ;
;
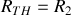 (car
(car
 est dans une branche ouverte).
est dans une branche ouverte).
2 -
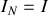 (car tout le courant issu du générateur passe dans le court-circuit) ;
(car tout le courant issu du générateur passe dans le court-circuit) ;
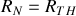 .
.
3 - Vérification évidente.
Circuit 1 :
1a - Le courant issu du générateur ne passe pas dans
 , puisqu'elle est dans une branche ouverte (on l'appelle "résistance morte"). Donc
, puisqu'elle est dans une branche ouverte (on l'appelle "résistance morte"). Donc
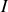 passe intégralement dans
passe intégralement dans
 , aux bornes de laquelle on mesure
, aux bornes de laquelle on mesure
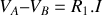 ou encore
ou encore
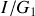 .
.
Remarque : vu des points
 et
et
 , la source de courant
, la source de courant
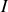 et la résistance
et la résistance
 en parallèle sur cette source constituent un générateur réel de courant, que l'on peut transformer en un générateur de tension en associant une fem
en parallèle sur cette source constituent un générateur réel de courant, que l'on peut transformer en un générateur de tension en associant une fem
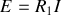 en série avec la résistance
en série avec la résistance
 . On obtient immédiatement
. On obtient immédiatement
 .
.
1b – Eteindre la source de courant dans le circuit veut dire remplacer le générateur de courant par un fil de résistance infinie (donc s'opposant au passage de tout courant).
Le circuit est alors celui dessiné ci-dessous, qui montre que
 et
et
 sont en parallèle entre
sont en parallèle entre
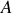 et
et
 .
.
Donc
 .
.
2 – Replaçons le générateur de courant dans le circuit, et relions
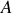 et
et
 par un fil sans résistance (court-circuit). Le courant
par un fil sans résistance (court-circuit). Le courant
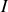 se partage en
se partage en
 en deux fractions
en deux fractions
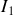 et
et
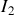 passant respectivement dans
passant respectivement dans
 et
et
 , de telle manière que les différences de potentiel aux bornes de chaque résistance soient identiques. On peut donc écrire aux bornes de
, de telle manière que les différences de potentiel aux bornes de chaque résistance soient identiques. On peut donc écrire aux bornes de

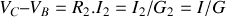 , avec
, avec
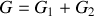 la conductance équivalente aux résistances
la conductance équivalente aux résistances
 et
et
 en parallèle.
en parallèle.
Soit
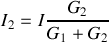 : on retrouve la relation du diviseur de courant, que l'on pouvait utiliser directement. Le courant
: on retrouve la relation du diviseur de courant, que l'on pouvait utiliser directement. Le courant
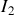 est aussi celui qui passe dans le court-circuit, donc
est aussi celui qui passe dans le court-circuit, donc
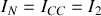 .
.
3 - On vérifie que
 .
.
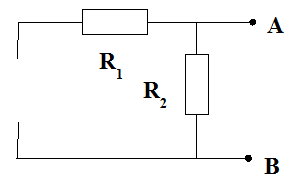
Circuit 2 :
1a - La fem
 du générateur de Thévenin est la différence de potentiel aux bornes de
du générateur de Thévenin est la différence de potentiel aux bornes de
 crée par le courant
crée par le courant
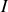 qui l'a traversée, donc on a tout de suite
qui l'a traversée, donc on a tout de suite
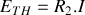 .
.
1b - Lorsque la source de courant est éteinte, le circuit est réduit à celui ci-dessous, où l'ont voit que la résistance entre les points
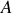 et
et
 est
est
 .
.
Donc
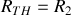 .
.
2 - Le fil sans résistance reliant
 et
et
 court-circuite la résistance
court-circuite la résistance
 , donc tout le courant
, donc tout le courant
 issu du générateur passe dans ce fil :
issu du générateur passe dans ce fil :
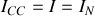 .
.
3 - La vérification est particulièrement rapide, puisque
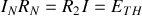 .
.



