Énoncé

Dans le circuit ci-dessus, établir l'expression du courant
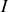 qui circule dans la résistance
qui circule dans la résistance
 , en précisant son sens,
, en précisant son sens,
1 - à l'aide des lois de Kirchhoff ;
2 - en appliquant le principe de superposition ;
3 - en transformant le circuit vu des points
 et
et
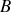 en un générateur de Thévenin ;
en un générateur de Thévenin ;
4 - en transformant le circuit vu des points
 et
et
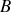 en un générateur de Norton.
en un générateur de Norton.
1 - Ecrire les équations donnant les courants circulant dans chaque branche en appliquant les lois de Kirchhoff, et résoudre ces équations pour trouver
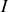 .
.
2 - Maintenir un générateur dans le circuit en éteignant tous les autres et trouvez le courant passant dans
 dû au seul générateur restant. Recommencer l'opération pour chaque autre générateur. Faire la somme des courants obtenus.
dû au seul générateur restant. Recommencer l'opération pour chaque autre générateur. Faire la somme des courants obtenus.
3 - Enlever la résistance
 et chercher la tension qui apparaît entre
et chercher la tension qui apparaît entre
 et
et
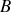 ; éteindre ensuite tous les générateurs et chercher la résistance qui apparaît entre
; éteindre ensuite tous les générateurs et chercher la résistance qui apparaît entre
 et
et
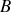 . En déduire
. En déduire
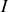 .
.
4 - Remplacer la résistance
 par un fil sans résistance et calculer le courant passant dans ce court-circuit ; puis, enlever ce fil, éteindre tous les générateurs et chercher la résistance qui apparaît entre
par un fil sans résistance et calculer le courant passant dans ce court-circuit ; puis, enlever ce fil, éteindre tous les générateurs et chercher la résistance qui apparaît entre
 et
et
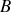 . En déduire
. En déduire
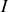 .
.
1 - Choisir arbitrairement des courants dans chaque branche du circuit ; écrire la loi des nœuds pour éliminer les variables en trop : il ne doit rester autant d'inconnues que de mailles élémentaires contenues dans le circuit (ici, deux).
Appliquer la loi des mailles en choisissant pour chacune un sens arbitraire de parcours. On obtient les équations (ici, deux) qui permettent de calculer algébriquement les courants inconnus. Résoudre ces équations avec les techniques classiques vues en mathématiques (élimination, substitution, déterminants ou autre).
2 - Lorsqu'il ne reste qu'un générateur dans le circuit, on peut facilement regrouper les résistances en utilisant les règles d'association en série et en parallèle. On en déduit la fraction
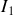 du courant
du courant
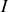 demandé due à ce seul générateur. On l'éteint alors, on en allume un second et on calcule la fraction
demandé due à ce seul générateur. On l'éteint alors, on en allume un second et on calcule la fraction
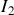 . Et ainsi de suite, autant de fois qu'il y a de générateurs dans le circuit. On obtient enfin le courant
. Et ainsi de suite, autant de fois qu'il y a de générateurs dans le circuit. On obtient enfin le courant
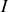 en faisant la somme algébrique
en faisant la somme algébrique
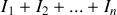 .
.
3 - Lorsque la résistance
 est enlevée, le reste du circuit crée entre les points
est enlevée, le reste du circuit crée entre les points
 et
et
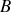 une différance de potentiel
une différance de potentiel
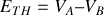 appelée force électromotrice de Thévenin, que l'on calcule en général facilement car le circuit amputé de
appelée force électromotrice de Thévenin, que l'on calcule en général facilement car le circuit amputé de
 a perdu une maille. Appliquer par exemple les lois de Kirchhoff.
a perdu une maille. Appliquer par exemple les lois de Kirchhoff.
Lorsque tous les générateurs sont éteints (et remplacés si besoin est par leur résistance interne), le circuit est devenu passif. La résistance
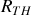 qui apparaît entre
qui apparaît entre
 et
et
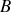 est appelée résistance de Thévenin. Elle se calcule en regroupant progressivement les résistances du circuit.
est appelée résistance de Thévenin. Elle se calcule en regroupant progressivement les résistances du circuit.
Lorsque
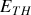 et
et
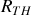 sont connus, on remplace le circuit par son générateur de Thévenin équivalent, sur lequel on branche
sont connus, on remplace le circuit par son générateur de Thévenin équivalent, sur lequel on branche
 . Le courant
. Le courant
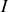 s'obtient alors sans difficulté.
s'obtient alors sans difficulté.
4 - Lorsque la résistance
 est enlevée et remplacée par un fil sans résistance, le reste du circuit crée dans ce fil un courant
est enlevée et remplacée par un fil sans résistance, le reste du circuit crée dans ce fil un courant
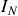 appelé courant de Norton, que l'on calcule en général facilement car le fait de réunir
appelé courant de Norton, que l'on calcule en général facilement car le fait de réunir
 et
et
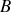 permet de négliger certaines portions du circuit. Appliquer par exemple les lois de Kirchhoff.
permet de négliger certaines portions du circuit. Appliquer par exemple les lois de Kirchhoff.
Lorsque tous les générateurs sont éteints (et remplacés si besoin est par leur résistance interne), le circuit est devenu passif. La résistance
 qui apparaît entre
qui apparaît entre
 et
et
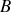 est appelée résistance de Norton. Elle se calcule en regroupant progressivement les résistances du circuit et elle est bien sûr égale à la résistance de Thévenin
est appelée résistance de Norton. Elle se calcule en regroupant progressivement les résistances du circuit et elle est bien sûr égale à la résistance de Thévenin
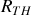 .
.
Lorsque
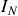 et
et
 sont connus, on remplace le circuit par son générateur de Norton équivalent, sur lequel on branche
sont connus, on remplace le circuit par son générateur de Norton équivalent, sur lequel on branche
 . Le courant
. Le courant
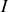 s'obtient alors sans difficulté.
s'obtient alors sans difficulté.
Réseaux électriques en régime continu : lois de Kirchhoff, principe de superposition, théorème de Thévenin, théorème de Norton.
Utiliser les explications du cours pour savoir mettre en œuvre quatre méthodes de résolution de circuits électriques.
1 - Appelons
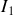 et
et
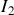 les courants passant respectivement dans les branches
les courants passant respectivement dans les branches
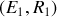 et
et
 . On les choisit arbitrairement, par exemple sortant de la borne
. On les choisit arbitrairement, par exemple sortant de la borne
 pour
pour
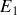 et sortant de la borne
et sortant de la borne
 pour
pour
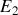 (mais tout autre choix conviendra). La résolution des équations obtenues en appliquant la loi des mailles donne
(mais tout autre choix conviendra). La résolution des équations obtenues en appliquant la loi des mailles donne
 ,
,
 ,
,
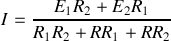 , de
, de
 vers
vers
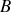 .
.
2 - Soit
 le courant passant dans
le courant passant dans
 de
de
 vers
vers
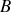 lorsque
lorsque
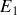 est seul à alimenter le circuit. On obtient
est seul à alimenter le circuit. On obtient
 .
.
En éteignant
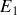 et en rallumant
et en rallumant
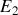 , on obtient de même
, on obtient de même
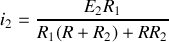 .
.
On retrouve la solution obtenue en
 en faisant
en faisant
 .
.
3 - Les éléments du générateur de Thévenin sont
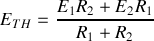 ,
,
 , soit
, soit
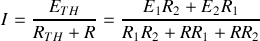
4 - Les éléments du générateur de Norton sont
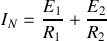 ,
,
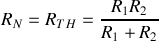 , soit
, soit
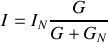 avec
avec
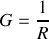 et
et
 .
.
1 –
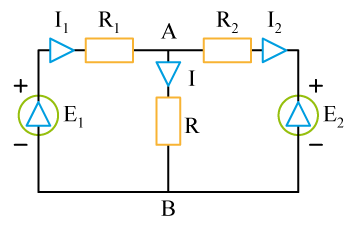
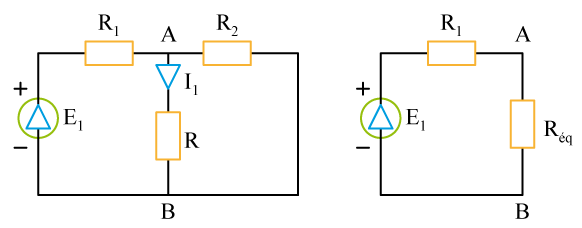
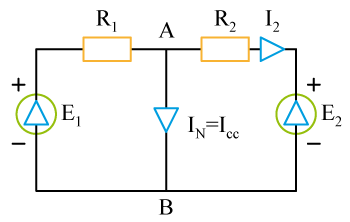
a) On choisit arbitrairement des courants dans chaque branche, par exemple comme sur la figure ci-dessus. La loi des nœuds s'écrit alors en

 qui fournit une relation entre les trois courants. On remarque qu'en
qui fournit une relation entre les trois courants. On remarque qu'en
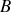 cette loi fournit la même relation. Il y a donc deux inconnues indépendantes, ce qui correspond bien au nombre de mailles élémentaires du circuit (maille élémentaire : plus petit parcours fermé que l'on peut effectuer sur le circuit ;
cette loi fournit la même relation. Il y a donc deux inconnues indépendantes, ce qui correspond bien au nombre de mailles élémentaires du circuit (maille élémentaire : plus petit parcours fermé que l'on peut effectuer sur le circuit ;
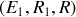 et
et
 sont des mailles élémentaires).
sont des mailles élémentaires).
On décide de conserver
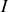 (puisque c'est la quantité demandée dans l'énoncé) et par exemple
(puisque c'est la quantité demandée dans l'énoncé) et par exemple
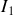 , donc on remplacera
, donc on remplacera
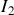 par
par
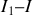 .
.
b) On écrit lois des mailles en parcourant les deux mailles élémentaires par exemple dans le sens trigonométrique en partant de
 , soit :
, soit :
 et
et
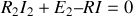 , qui donne
, qui donne
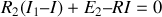 .
.
Le système d'équations à résoudre est donc
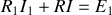

c) Plusieurs méthodes permettent de résoudre ce système. Rappelons sa solution :
Le système
 et
et
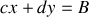 a pour solution
a pour solution
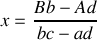 et
et
 .
.
On en déduit l'expression des courants
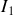 et
et
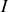 :
:
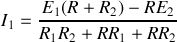 et
et
 donc on tire
donc on tire
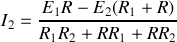 .
.
Remarque :
le courant
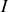 , calculé ici de
, calculé ici de
 vers
vers
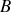 , est toujours positif. En revanche les courants
, est toujours positif. En revanche les courants
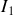 et
et
 peuvent avoir le sens choisi arbitrairement ou le sens inverse, selon les valeurs des composants du circuit.
peuvent avoir le sens choisi arbitrairement ou le sens inverse, selon les valeurs des composants du circuit.
2)
a)
Enlevons
 et appelons
et appelons
 le courant qui circule dans
le courant qui circule dans
 dans cette situation. On peut remplacer les résistances
dans cette situation. On peut remplacer les résistances
 et
et
 , branchées en parallèle, par leur résistance équivalente
, branchées en parallèle, par leur résistance équivalente
 .
.
Le circuit se présenta alors comme un diviseur de tension et on peut exprimer facilement la différence de potentiel entre
 et
et
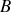 :
:
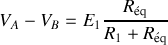 .
.
Il ne reste plus qu'à écrire
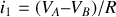 , soit après calcul :
, soit après calcul :
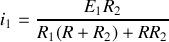 .
.
b) On éteint
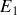 et on rallume
et on rallume
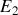 . On retrouve alors un circuit identique au précédent, donc inutile de refraire le calcul
. On retrouve alors un circuit identique au précédent, donc inutile de refraire le calcul
 Il suffit de permuter les rôles de
Il suffit de permuter les rôles de
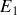 et
et
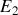 , ainsi que ceux des résistances
, ainsi que ceux des résistances
 et
et
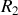 . On obtient directement
. On obtient directement
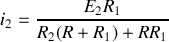 .
.
c) Il ne reste plus qu'à écrire
 pour retrouver le résultat.
pour retrouver le résultat.
3)
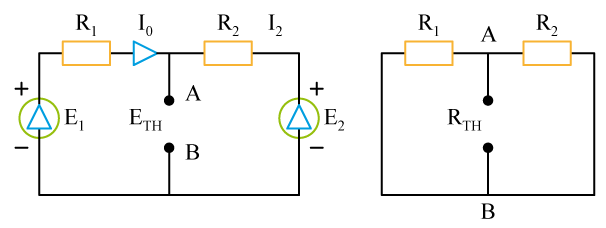
a) Enlevons la résistance
 . La différence de potentiel qui apparaît entre
. La différence de potentiel qui apparaît entre
 et
et
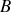 est la force électromotrice
est la force électromotrice
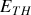 du générateur équivalent de Thévenin. On la calcule par l'intermédiaire du courant
du générateur équivalent de Thévenin. On la calcule par l'intermédiaire du courant
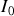 qui circule dans le circuit. On choisit son sens arbitrairement et la loi des mailles donne
qui circule dans le circuit. On choisit son sens arbitrairement et la loi des mailles donne
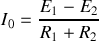 , soit
, soit
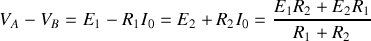 .
.
b) On éteint maintenant les deux générateurs. Le circuit est devenu passif et il reste entre
 et
et
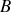 une résistance qui est celle du générateur de tension équivalent. On voit facilement que
une résistance qui est celle du générateur de tension équivalent. On voit facilement que
 et
et
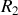 sont reliées en parallèle entre
sont reliées en parallèle entre
 et
et
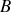 , donc
, donc
 .
.
c)
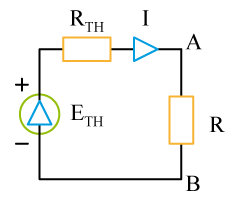
Le courant
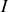 cherché s'obtient facilement en remplaçant le circuit initial par son générateur équivalent, selon le schéma ci-contre :
cherché s'obtient facilement en remplaçant le circuit initial par son générateur équivalent, selon le schéma ci-contre :
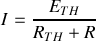 soit
soit
 .
.
4)
a) Enlevons la résistance
 et remplaçons-la par un fil sans résistance, appelé aussi court-circuit. Le courant Icc qui passe dans ce fil est le courant du générateur de Norton équivalent au circuit vu des points
et remplaçons-la par un fil sans résistance, appelé aussi court-circuit. Le courant Icc qui passe dans ce fil est le courant du générateur de Norton équivalent au circuit vu des points
 et
et
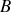 . On le calcule facilement, puisqu'il est la somme des courants délivrés par chacun des générateurs :
. On le calcule facilement, puisqu'il est la somme des courants délivrés par chacun des générateurs :
 .
.
b) Enlevons le court-circuit et éteignons les deux générateurs. On retrouve le circuit passif déjà rencontré en appliquant le théorème de Thévenin. La résistance qui apparaît entre
 et
et
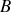 est donc la même :
est donc la même :
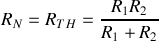 .
.
c)

Remplaçons le circuit par son générateur de courant équivalent vu entre les points
 et
et
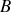 , et replaçons la résistance
, et replaçons la résistance
 .
.
Le courant
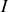 s'obtient facilement en regroupant les résistances
s'obtient facilement en regroupant les résistances
 et
et
 branchées en parallèle, soit
branchées en parallèle, soit
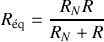 , puis en écrivant
, puis en écrivant
 et enfin
et enfin
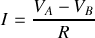 , ce qui revient à appliquer la relation du diviseur de courant :
, ce qui revient à appliquer la relation du diviseur de courant :
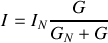 , avec
, avec
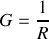 et
et
 .
.
On retrouve alors la solution
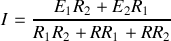 .
.



