Énoncé

Soit le groupement ci dessus, dans lequel les résistances valent
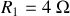 ,
,
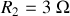 ,
,
 ,
,
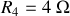 .
.
1 - Calculez la résistance équivalente au groupement, entre les points
 et
et
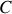 .
.
2 - On relie
 et
et
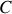 aux pôles respectivement positif et négatif d'un générateur de fem
aux pôles respectivement positif et négatif d'un générateur de fem
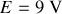 . Calculez l'intensité des courants passant dans chaque résistance.
. Calculez l'intensité des courants passant dans chaque résistance.
3 - Calculez la puissance électrique fournie par ce générateur, puis la puissance dissipée dans chacune des résistances. Conclusion ?
La résistance totale du circuit donne le courant fourni par le générateur lorsque celui-ci est relié aux points
 et
et
 . Calculer alors les courants passant dans chaque résistance et en déduire la puissance électrique consommée par chacune d'elles.
. Calculer alors les courants passant dans chaque résistance et en déduire la puissance électrique consommée par chacune d'elles.
Calculer la résistance équivalente au groupement, en utilisant les lois d'association des résistances. Lorsque le générateur est branché entre
 et
et
 , on obtient facilement le courant qu'il fournit grâce à la résistance totale du circuit, ainsi que les fractions de ce courant passant dans
, on obtient facilement le courant qu'il fournit grâce à la résistance totale du circuit, ainsi que les fractions de ce courant passant dans
 ,
,
 et
et
 . On applique alors les relations vues dans le cours qui donnent la puissance fournie par le générateur et celle consommée dans chaque résistance. Puis faire le bilan énergétique, en comparant la puissance fournie par le générateur et celle consommée par l'ensemble du circuit.
. On applique alors les relations vues dans le cours qui donnent la puissance fournie par le générateur et celle consommée dans chaque résistance. Puis faire le bilan énergétique, en comparant la puissance fournie par le générateur et celle consommée par l'ensemble du circuit.
Généralités : Puissance électrique.
Les composants électriques dipolaires : dipôles passifs, dipôles actifs.
Exercice de référence sur les diviseurs de tension et de courant.
Utiliser les relations du cours exprimant la puissance fournie par un générateur et celle reçue par un récepteur. Le bilan énergétique doit s'écrire : somme des puissance fournies par chaque générateur = somme des puissances consommées par chaque récepteur.
1 - La résistance totale
 équivalente aux cinq résistances du circuit est
équivalente aux cinq résistances du circuit est
 . Entre
. Entre
 et
et
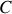 , la résistance est
, la résistance est
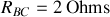 .
.
2 – Le courant fourni par le générateur est
 . C'est aussi celui qui passe dans
. C'est aussi celui qui passe dans
 .
.
Les courants
 et
et
 passant dans
passant dans
 et
et
 ou
ou
 peuvent être obtenus rapidement avec la relation du diviseur de courant, en posant
peuvent être obtenus rapidement avec la relation du diviseur de courant, en posant
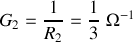 et
et
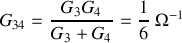 .
.
Soit
 , et
, et
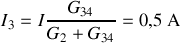 .
.
3 – Puissance fournie par le générateur :
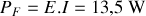 .
.
Puissances consommées dans les résistances : on applique la relation
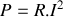 , soit
, soit
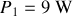 ;
;
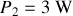 ;
;
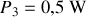 ;
;
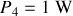 .
.
On vérifie bien que
 .
.
1 - Calculons d'abord la résistance équivalente
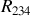 entre les points
entre les points
 et
et
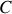 , en appelant
, en appelant
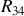 celle qui remplace les résistances
celle qui remplace les résistances
 et
et
 placées en série, soit
placées en série, soit
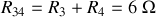 .
.
Les résistances
 et
et
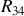 sont en parallèle, donc
sont en parallèle, donc
 .
.
On additionne
 à
à
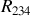 pour obtenir
pour obtenir
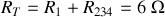 .
.
2 - En remplaçant, entre
 et
et
 , les quatre résistances par leur résistance totale
, les quatre résistances par leur résistance totale
 , on obtient un circuit plus simple dans lequel le générateur est en série avec
, on obtient un circuit plus simple dans lequel le générateur est en série avec
 . On en déduit le courant
. On en déduit le courant
 qu'il fournit au circuit :
qu'il fournit au circuit :
 .
.
Ce courant est aussi celui,
 , qui passe dans
, qui passe dans
 (ainsi que dans
(ainsi que dans
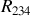 ), donc
), donc
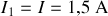 .
.
Pour trouver les courants
 et
et
 passant respectivement dans
passant respectivement dans
 et
et
 (ou aussi
(ou aussi
 ), on peut calculer la différence de potentiel
), on peut calculer la différence de potentiel
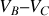 existant entre les points
existant entre les points
 et
et
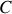 en utilisant la relation du diviseur de tension :
en utilisant la relation du diviseur de tension :
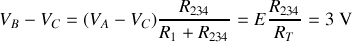 .
.
On en tire immédiatement
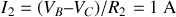 , et
, et
 .
.
Remarque 1 : on vérifie bien que
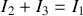 .
.
Remarque 2 : on peut aussi calculer
 et
et
 en utilisant la relation du diviseur de courant (voir solution rapide).
en utilisant la relation du diviseur de courant (voir solution rapide).
3 - Il ne reste plus qu'à appliquer les relations du cours : la puissance fournie par un générateur de fem
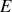 et délivrant le courant
et délivrant le courant
 est
est
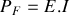 , et la puissance reçue par une résistance
, et la puissance reçue par une résistance
 parcourue par le courant
parcourue par le courant
 est
est
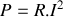 .
.
Ce qui donne :
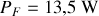 ;
;
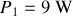 ;
;
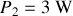 ;
;
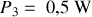 ;
;
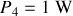 .
.
A la différence d'un condensateur ou d'une bobine d'induction, une résistance n'emmagasine pas d'énergie : elle transforme instantanément ce qu'elle reçoit en chaleur. Le bilan énergétique impose donc
 .
.
Cette relation est vérifiée ici.



