Énoncé
Trois lampes à incandescence de puissances différentes (par exemple
,
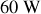et
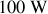) sont reliées en série ; l'ensemble est branché sur un générateur délivrant une à une tension de
. En admettant que l'éclairement d'une lampe est proportionnel à la puissance électrique qu'elle reçoit, quelle lampe brillera le plus fort ?
Comparer les résistances de chaque lampe pour pouvoir évaluer la puissance électrique que chacune reçoit du générateur.
Rappel de cours :
Généralités : Puissance électrique.
Les composants électriques dipolaires : dipôles passifs, dipôles actifs.
Les lampes sont placées en série, donc sont parcourues par le même courant électrique. C'est donc la lampe dont la résistance est la plus grande qui reçoit la plus grande puissance et donc brille le plus.
La résistance d'une lampe peut être évaluée par la relation
, où
est sa puissance nominale et
sa tension d'utilisation, soit
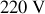. C'est donc la lampe qui a la résistance la plus faible qui correspond à la puissance nominale la plus élevée. Ainsi,
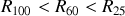. Lorsque les lampes sont branchées en série, elles sont parcourues par le même courant
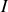, et c'est celle qui a la résistance la plus grande qui reçoit la plus grande part de la puissance fournie par le générateur. C'est donc la lampe de
qui brillera le plus fort.
L'exercice est volontairement posé pour guider le lecteur vers une mauvaise réponse (la réponse intuitive est la lampe de
). L'explication est pourtant simple et l'expérience facile à réaliser.
Appelons
la puissance nominale d'une lampe (celle qui est fournie par le constructeur), et
sa tension normale d'utilisation (donc
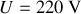). La relation liant
et
est
, où
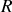est la résistance de la lampe. Elle montre que pour une tension
fixée, la résistance
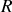d'une lampe est d'autant plus petite que sa puissance est élevée. On peut donc classer les résistances des trois lampes de l'énoncé comme suit :
.
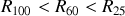Si ces lampes étaient branchées en parallèle sur le générateur (cas d'une utilisation domestique normale), elles seraient soumises à la même tension
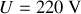et donc recevraient du circuit une puissance électrique égale à leur puissance nominale ; c'est donc la lampe de puissance
qui brillerait le plus. Or dans cette expérience les lampes sont reliées en série : c'est le courant qui les traverse qui reste constant, et la différence de potentiel à leurs bornes est d'autant plus petite que leur résistance est faible. On peut donc écrire
.
La puissance électrique reçue par chaque lampe est
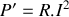; elle est différente de la puissance nominale
et est d'autant plus petite que la résistance
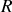de la lampe est faible: c'est donc la lampe de
qui brille le moins.
Voici une application numérique pour fixer les idées :
• Calcul de la résistance
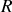d'une lampe connaissant sa puissance nominale
sous une tension d'utilisation
:
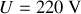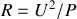, soit
,
,
.
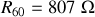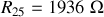• Calcul du courant
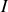traversant les lampes placées en série sur la tension
:
, soit
.
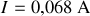• Pour information, calculons les tensions aux bornes de chaque lampe
:
,
,
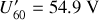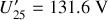, le total des trois redonnant bien sûr
.
• Calcul de la puissance
reçue du circuit par chaque lampe :
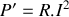, soit
,
,
.
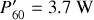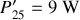On voit que dans cette situation, les puissances lumineuses sont bien inférieures à celles annoncées par le constructeur : la lampe de
ne s'allumera quasiment pas, la lampe de
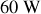brillera légèrement. Seule la lampe de
sera franchement allumée, mais émettra moins de lumière que dans son utilisation normale sous la tension de
.
Remarque :
Les résistances calculées ci-dessus sont celles des filaments lorsque ceux-ci sont portés à incandescence. Si on mesure avec un ohmmètre la résistance d'une lampe, on trouvera une valeur bien plus faible : c'est que la résistance du filament de tungstène augmente avec la température, ce qui limite le courant qui le traverse. Lorsque le filament est chaud, l'intensité du courant est de l'ordre d'une fraction d'ampère (
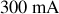pour la lampe de
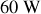). Au moment de l'allumage, le filament est froid et ce courant peut, durant une fraction de seconde, être bien plus important. C'est pourquoi les lampes a filament de tungstène "claquent" presque toujours lorsqu'on les met sous tension.
