Énoncé
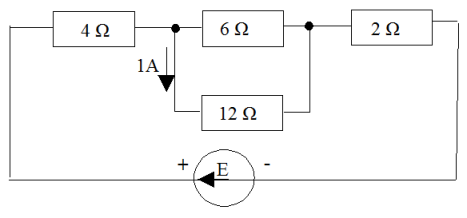
Dans le schéma ci-dessus, compte tenu de la valeur de l'intensité qui circule dans la résistance de
 , on demande la valeur de la force électromotrice
, on demande la valeur de la force électromotrice
 du générateur de tension qui alimente le circuit.
du générateur de tension qui alimente le circuit.

Dans le schéma ci-dessus, compte tenu de la valeur de l'intensité qui circule dans la résistance de
 , on demande la valeur de la force électromotrice
, on demande la valeur de la force électromotrice
 du générateur de tension qui alimente le circuit.
du générateur de tension qui alimente le circuit.
Calculer le courant délivré par le générateur, puis la résistance équivalente branchée à ses bornes, et en déduire la valeur de sa fem.
Rappel de cours :
Généralités : loi des nœuds, loi des mailles.
Les composants électriques dipolaires : lois d'association des résistors.
Connaissant le courant
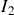 traversant la résistance de
traversant la résistance de
 , calculer le courant
, calculer le courant
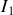 passant dans la résistance de
passant dans la résistance de
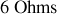 placée en parallèle. On en déduit le courant total
placée en parallèle. On en déduit le courant total
 fourni par le générateur.
fourni par le générateur.
Calculer la résistance équivalente
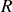 branchée sur le générateur et en déduire
branchée sur le générateur et en déduire
 .
.
Le courant passant dans la résistance de
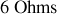 vaut deux fois celui qui passe dans celle de
vaut deux fois celui qui passe dans celle de
 , soit
, soit
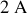 . Le générateur délivre dont un courant
. Le générateur délivre dont un courant
 de
de
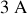 .
.
La résistance totale du circuit est
 , donc
, donc
 .
.
Appelons
 et
et
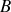 les extrémités du groupement des deux résistances
les extrémités du groupement des deux résistances
 et
et
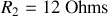 . On peut écrire
. On peut écrire
 de deux façons :
de deux façons :
avec le courant
 passant dans la résistance
passant dans la résistance
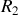 , soit
, soit
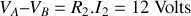 ;
;
avec le courant
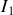 passant dans
passant dans
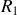 , soit
, soit
 , ce qui donne
, ce qui donne
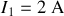 .
.
Le courant qui arrive au point
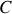 , avant de se séparer en
, avant de se séparer en
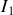 et
et
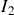 , vaut donc
, vaut donc
 .
.
Calculons maintenant la résistance totale du circuit, sur laquelle le générateur est branché :
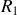 et
et
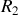 en parallèle sont équivalente à une résistance valant
en parallèle sont équivalente à une résistance valant
 . La résistance totale du circuit vaut donc
. La résistance totale du circuit vaut donc
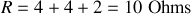 .
.
Pour que le générateur de fem
 puisse fournir un courant
puisse fournir un courant
 de
de
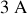 dans une résistance
dans une résistance
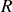 de
de
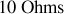 , il faut que
, il faut que
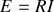 , ce qui donne
, ce qui donne
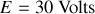 .
.



