Énoncé

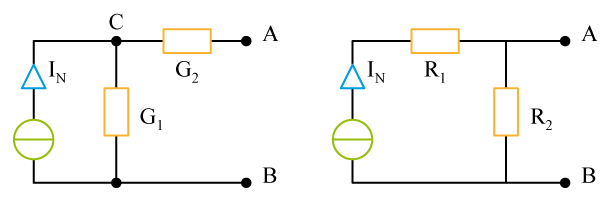
1 - Remplacer le circuit 1 par son générateur équivalent de Thévenin.
2 - En déduire l'intensité du courant
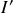 qui traverse la résistance
qui traverse la résistance
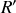 dans le circuit 2, en précisant son sens de parcours (de
dans le circuit 2, en précisant son sens de parcours (de
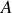 vers
vers
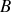 ou de
ou de
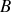 vers
vers
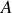 )..
)..
1 - Aucune difficulté pour trouver
 en utilisant le diviseur de tension. Pour trouver
en utilisant le diviseur de tension. Pour trouver
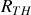 , remplacer le générateur par un fil sans résistance.
, remplacer le générateur par un fil sans résistance.
2 - Remplacer la partie gauche du circuit par le générateur de Thévenin vu en 1. Le calcul de
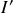 se fait facilement en appliquant la loi des mailles.
se fait facilement en appliquant la loi des mailles.
Rappel de cours :
Réseaux électriques en régime continu : théorème de Thévenin.
Exercice de référence "un circuit à mettre en équation par quatre méthodes".
Exercice de référence sur les diviseurs de tension et de courant.
1 -
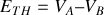 s'obtient soit en exprimant le courant
s'obtient soit en exprimant le courant
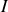 qui sort du générateur de fem
qui sort du générateur de fem
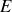 puis en écrivant
puis en écrivant
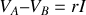 , soit plus simplement en utilisant le diviseur de tension
, soit plus simplement en utilisant le diviseur de tension
 .
.
Lorsqu'on éteint la fem
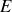 , les résistances
, les résistances
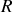 et
et
 sont branchées en parallèle entre
sont branchées en parallèle entre
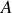 et
et
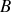 , et leur résistance équivalente donne
, et leur résistance équivalente donne
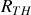 .
.
2 - Remplacer la partie gauche du circuit par le générateur de Thévenin vu en 1 : on obtient un circuit plus simple ne comportant qu'une seule maille et parcouru par le courant
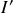 demandé. Choisir un sens de parcours pour
demandé. Choisir un sens de parcours pour
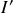 et appliquer la loi des mailles.
et appliquer la loi des mailles.
1 - Le diviseur de tension
 donne
donne
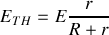 ;
;
 .
.
2 - Choisissons le sens de passage de
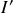 de
de
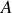 vers
vers
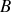 dans
dans
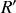 : la loi des mailles donne
: la loi des mailles donne
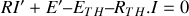 , dont on tire
, dont on tire
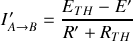 .
.
1 - Appelons
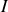 le courant qui circule dans le circuit 1 : la loi des mailles donne facilement
le courant qui circule dans le circuit 1 : la loi des mailles donne facilement
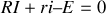 , soit
, soit
 . On obtient alors
. On obtient alors
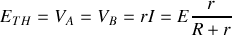 .
.
On pouvait bien sûr écrire ceci directement en utilisant le diviseur de tension
 .
.
En remplaçant la source de tension
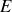 par un fil sans résistance, on constate que les résistances
par un fil sans résistance, on constate que les résistances
 et
et
 sont branchées en parallèle entre
sont branchées en parallèle entre
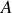 et
et
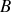 : la résistance
: la résistance
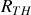 vue entre les points
vue entre les points
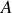 et
et
 est donc la résistance équivalente à leur groupement, soit
est donc la résistance équivalente à leur groupement, soit
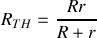 .
.
2 - L'intérêt du générateur équivalent est qu'il peut remplacer le circuit à partir duquel on l'a déterminé, à gauche des points
 et
et
 . Remplaçons donc, dans le circuit 2,
. Remplaçons donc, dans le circuit 2,
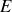 ,
,
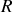 et
et
 par le générateur de Thévenin vu en 1. On obtient ainsi un circuit plus simple, ne comportant qu'une seule maille et parcouru par le courant
par le générateur de Thévenin vu en 1. On obtient ainsi un circuit plus simple, ne comportant qu'une seule maille et parcouru par le courant
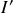 demandé.
demandé.
Pour trouver
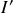 , il faut appliquer la loi des mailles en choisissant d'abord un sens de passage : par exemple,
, il faut appliquer la loi des mailles en choisissant d'abord un sens de passage : par exemple,
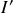 traverse
traverse
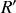 de
de
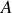 vers
vers
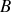 . En appliquant les règles pratiques vues dans le chapitre 2, on écrit, en faisant un tour complet de
. En appliquant les règles pratiques vues dans le chapitre 2, on écrit, en faisant un tour complet de
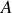 vers
vers
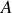 ,
,
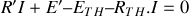 , ce qui donne
, ce qui donne
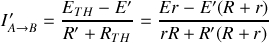
Remarque : 1
Le sens réel de passage du courant
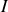 dans le circuit 2 dépend de la valeur numérique de ses composants : si
dans le circuit 2 dépend de la valeur numérique de ses composants : si
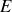 ,
,
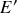 ,
,
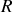 et
et
 sont tels que
sont tels que
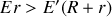 , alors le sens choisi arbitrairement est le bon, sinon c'est le contraire. Si
, alors le sens choisi arbitrairement est le bon, sinon c'est le contraire. Si
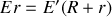 , ce qui revient à écrire
, ce qui revient à écrire
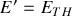 , alors aucun courant ne parcourt la branche
, alors aucun courant ne parcourt la branche
 : tout le courant sortant du générateur
: tout le courant sortant du générateur
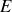 passe intégralement dans la résistance
passe intégralement dans la résistance
 .
.
Remarque : 2
Le circuit 2 pouvait aussi être mis en équation en appliquant plusieurs autres méthodes : voir le corrigé de l'exercice de référence "un circuit à mettre en équation par quatre méthodes" : on y retrouve un circuit identique, en y faisant
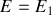 ,
,
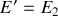 ,
,
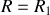 ,
,
 et
et
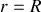 .
.



