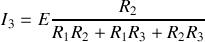Énoncé
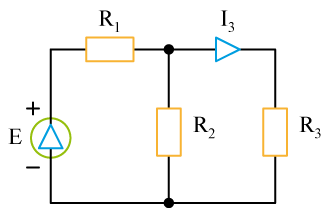
Soit le circuit ci-dessus, alimenté par un générateur de fem
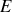 sans résistance interne.
sans résistance interne.
Calculer le courant
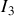 passant dans la résistance
passant dans la résistance
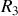 en fonction des composants du circuit.
en fonction des composants du circuit.
Le plus rapide : regrouper
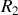 et
et
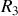 en une résistance unique
en une résistance unique
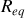 et exploiter le diviseur de tension
et exploiter le diviseur de tension
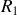 ,
,
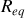 pour exprimer la différence de potentiel aux bornes de
pour exprimer la différence de potentiel aux bornes de
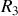 . En déduire
. En déduire
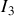 .
.
Rappel de cours :
Généralités : loi des nœuds, loi des mailles.
Les composants électriques dipolaires : lois d'association des résistors, source de tension (ou générateur idéal).
Exercice de référence sur les diviseurs de tension et de courant.
Lorsque deux résistances
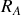 et
et
 sont branchées en série et que l'ensemble est relié à une source de tension
sont branchées en série et que l'ensemble est relié à une source de tension
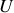 , la différence de potentiel aux bornes de
, la différence de potentiel aux bornes de
 est
est
 (voir l'exercice de référence sur les diviseurs de tension).
(voir l'exercice de référence sur les diviseurs de tension).
En posant
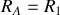 et
et
 la résistance équivalente à
la résistance équivalente à
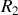 et
et
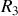 (reliées en parallèle), on obtient facilement la différence de potentiel
(reliées en parallèle), on obtient facilement la différence de potentiel
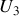 aux bornes de
aux bornes de
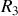 . On écrit alors
. On écrit alors
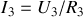 .
.
Celle-ci se fait en trois étapes :
a) Regroupons
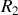 et
et
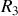 en une résistance unique
en une résistance unique
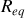 : on obtient
: on obtient
 .
.
b) Notons
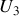 la différence de potentiel aux bornes de
la différence de potentiel aux bornes de
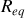 : celle-ci se calcule facilement avec la relation du diviseur de tension constitué par
: celle-ci se calcule facilement avec la relation du diviseur de tension constitué par
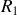 et
et
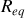 :
:

c) On écrit enfin
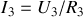 , ce qui donne tous calculs faits
, ce qui donne tous calculs faits
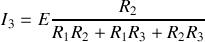
Appelons
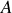 le pôle positif du générateur,
le pôle positif du générateur,
 son pôle négatif et
son pôle négatif et
 le point commun aux résistances
le point commun aux résistances
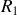 ,
,
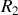 et
et
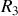 .
.
Lorsqu'un circuit alimenté en régime continu ne contient qu'un seul générateur, il est pratiquement toujours possible de prévoir le sens de passage des courants dans chacune des branches, car elles ne contiennent que des résistances (la seule exception est un circuit contenant des résistances placées en triangle). Ainsi dans le circuit proposé passe de
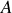 vers
vers
 dans
dans
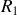 , de
, de
 vers
vers
 dans
dans
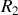 et
et
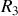 . L'expression algébrique de
. L'expression algébrique de
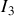 orienté comme sur le schéma doit conduire à un résultat positif.
orienté comme sur le schéma doit conduire à un résultat positif.
Il y a trois (au moins) manières de calculer
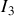 : la première, immédiate, consiste à utiliser la relation du diviseur de tension ; la seconde, moins intuitive, est d'appliquer la relation du diviseur de courant ; la troisième, longue et fastidieuse, est de mettre le circuit en équation en utilisant les lois de Kirchhoff, ou les théorème de Thévenin ou de Norton (cf chapitre III). Nous ne donnerons ici que les deux premières.
: la première, immédiate, consiste à utiliser la relation du diviseur de tension ; la seconde, moins intuitive, est d'appliquer la relation du diviseur de courant ; la troisième, longue et fastidieuse, est de mettre le circuit en équation en utilisant les lois de Kirchhoff, ou les théorème de Thévenin ou de Norton (cf chapitre III). Nous ne donnerons ici que les deux premières.
1 – Utilisation du diviseur de tension :
Il apparaît facilement si on regroupe les résistances
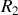 et
et
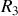 . Elles sont en parallèles, donc
. Elles sont en parallèles, donc
 , soit
, soit
 .
.
Le circuit peut alors être redessiné en remplaçant
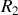 et
et
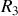 par
par
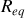 , et on applique la relation du diviseur de tension pour obtenir la différence de potentiel
, et on applique la relation du diviseur de tension pour obtenir la différence de potentiel
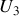 aux bornes de
aux bornes de
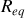 :
:
 .
.
Or
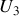 est aussi la différence de potentiel existant aux bornes de
est aussi la différence de potentiel existant aux bornes de
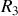 (et aussi de
(et aussi de
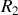 ), ce qui permet d'écrire le courant
), ce qui permet d'écrire le courant
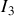 passant dans
passant dans
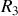 :
:
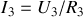 (si on avait demandé le courant
(si on avait demandé le courant
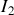 passant dans
passant dans
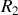 , on aurait écrit
, on aurait écrit
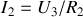 ).
).
On obtient ainsi, en remplaçant
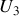 puis
puis
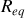 par leurs expressions :
par leurs expressions :
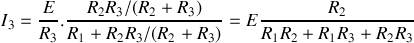
2 – Utilisation du diviseur de courant :
Soit
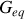 la conductance équivalente à
la conductance équivalente à
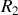 et
et
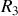 branchées en parallèle :
branchées en parallèle :
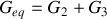 .
.
On écrit alors l'expression du courant
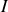 sortant du générateur (donc traversant
sortant du générateur (donc traversant
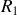 ) :
) :
 .
.
Il ne reste plus qu'à appliquer la relation du diviseur de courant (voir l'exercice de référence) :
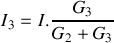 .
.
On retrouve sans difficulté l'expression de
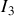 :
: