Fondamental :
Enoncé : lorsque un point matériel
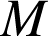se déplace dans un champ de forces conservatif (dérivant d'un potentiel
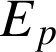), son énergie mécanique
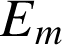définie par la relation
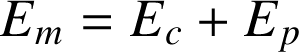
reste constante au cours du mouvement.
En effet, le théorème de l'énergie cinétique s'écrit (section 5.2) :
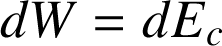
Par ailleurs, pour un champ de force conservatif (section 5.3) :
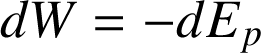
En soustrayant les deux relations membre à membre, on obtient :
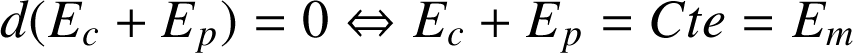
Exemple :
L'énergie mécanique associée au ressort horizontal.
Etirons le ressort en
. A l'instant où on le relâche, la vitesse initiale est nulle et son élongation est maximale (elle vaut
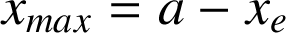). Par contre lorsqu'il repasse par sa position d'équilibre
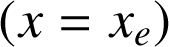, son élongation est nulle. La conservation de l'énergie mécanique nous permet d'affirmer qu'en cette position d'équilibre, la vitesse de la masse
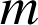accrochée au ressort sera maximale :
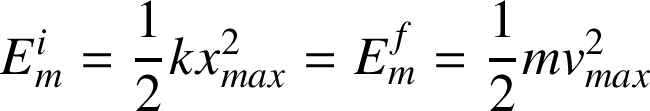
Soit
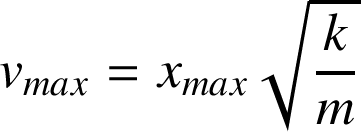
Exemple :
l'oscillateur harmonique (cas général).
Cette étude va nous permettre d'obtenir l'équation du mouvement d'un point M en faisant l'hypothèse que les oscillations de M se font autour d'une position d'équilibre stable. On suppose applicable le théorème de l'énergie mécanique (forces conservatives, à vérifier pour chaque problème considéré) :
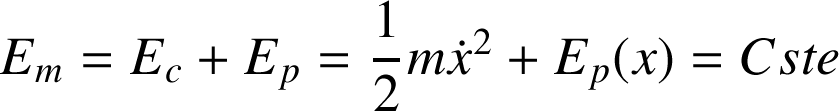
On est intéressé par le mouvement d'oscillations autour d'une position d'équilibre stable. Développons la fonction
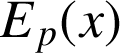en série de Taylor autour du minimum
:
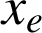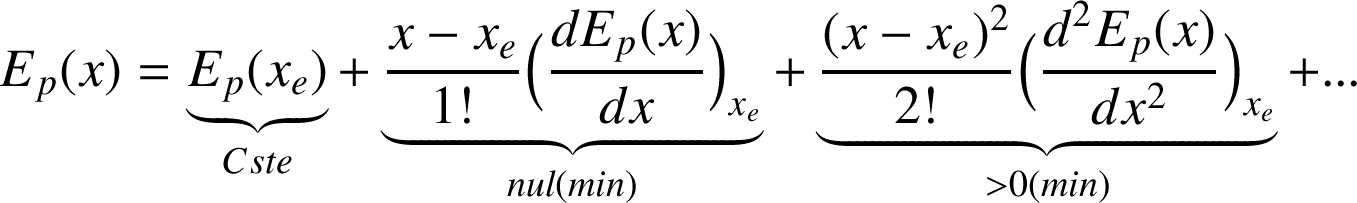
On a donc :
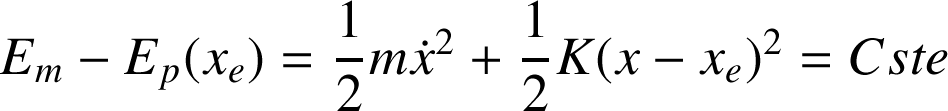
Avec
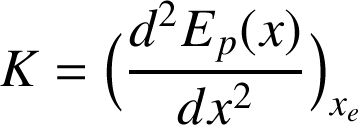
Notons au passage qu'en dérivant cette expression, on obtient l'équation du mouvement de M :
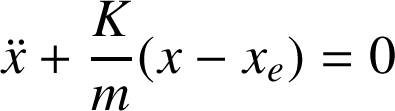
En changeant de variable
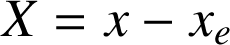, on se ramène à l'équation canonique :
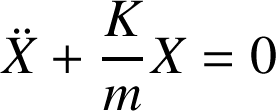
Remarque :
L'énergie mécanique étant constante, il y a au cours du temps des transferts d'énergie, entre le terme cinétique et le terme potentiel. Montrons-le pour l'oscillateur harmonique !
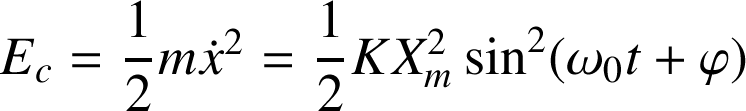
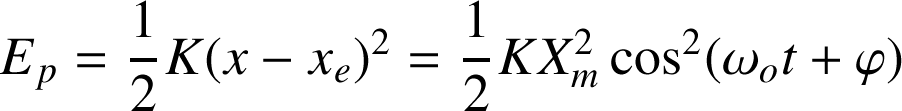
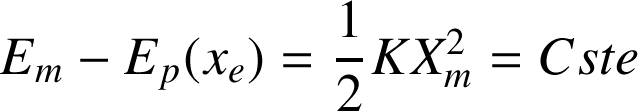
Graphiquement :
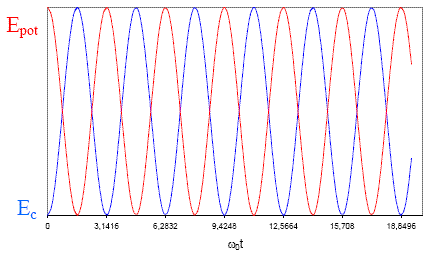
En résumé, pour une force conservative (en pratique toutes les forces considérées dans ce cours de première année à l'exception des forces de frottement), le principe de conservation de l'énergie mécanique d'un point matériel implique qu'il y a transformation de l'énergie cinétique en énergie potentielle, et réciproquement.
Fondamental :
Cas général
En général un objet est soumis à un ensemble de forces, conservatives et non-conservatives. Une manière élégante de traiter le problème énergétique est de passer par la notion de travail.
Décomposons le travail élémentaire
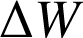en deux contributions, associées aux travaux des forces conservatives et non conservatives, respectivement :
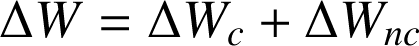
La contribution associée aux forces conservatives peut s'exprimer en fonction de leurs énergies potentielles :
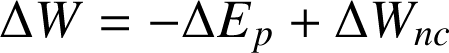
Par ailleurs appliquons le théorème de l'énergie cinétique à
:
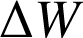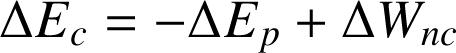
En regroupant les termes qui permettent d'introduire l'énergie mécanique, on obtient :
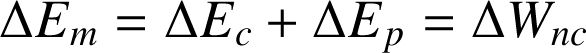
C'est une relation qui exprime que la variation de l'énergie mécanique est égale au travail des forces non-conservatives :
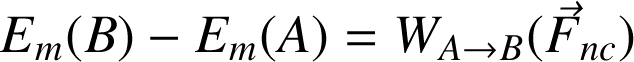
Exemple :
Application. Mouvement à force centrale conservative. Mouvement d'un satellite.
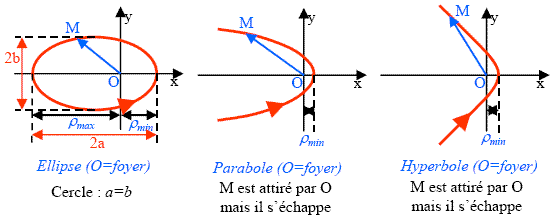
Cette application va nous permettre d'illustrer les lois de Kepler (1604 et 1618) :
Les orbites (trajectoires) des planètes sont des ellipses dont le Soleil est un foyer.
Le rayon vecteur
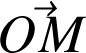issu du Soleil balaie des aires égales pendant des durées égales (loi des aires).Les carrés des périodes de révolution sont proportionnels aux cubes des demigrands axes de l'ellipse :
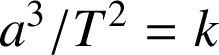
On se limite à la force newtonienne de gravitation. Ainsi, un point matériel M de masse
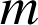subit de O une force de gravitation :
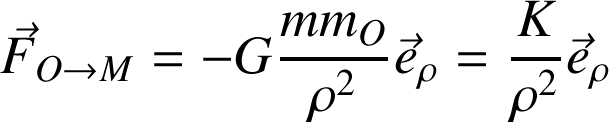
avec
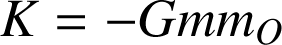
et
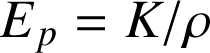
L'énergie mécanique est conservée :
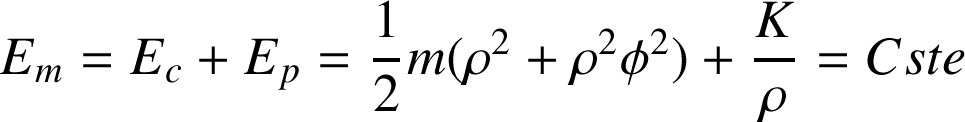
Nous rappelons que pour un mouvement à accélération centrale (section 3.4), le mouvement se fait dans un plan et la grandeur suivante est une constante :
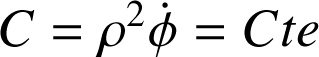
On peut donc exprimer l'énergie mécanique sous la forme :
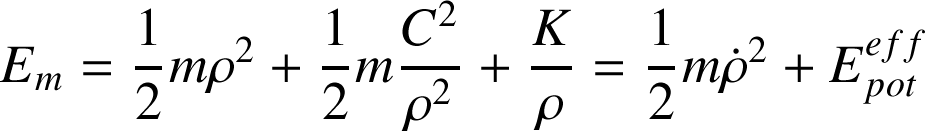
L'énergie mécanique est donc la somme de deux contributions. La première est toujours définie positive et s'ajoutera à la seconde
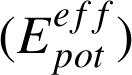, qui est représentée schématiquement sur la figure ci-dessous.
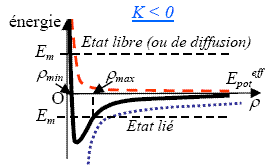
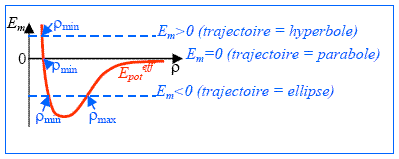
Quelle est la trajectoire (plane) du point matériel M soumis à ce type de force ?
Résoudre l'équation du mouvement est hors programme. Graphiquement, retenons :
Définition :
Vitesse de libération
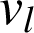
C'est la vitesse minimale du point M qui lui permet de s'échapper de sa trajectoire elliptique (ou circulaire). La condition requise pour cela est
.
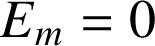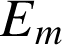s'écrit alors :
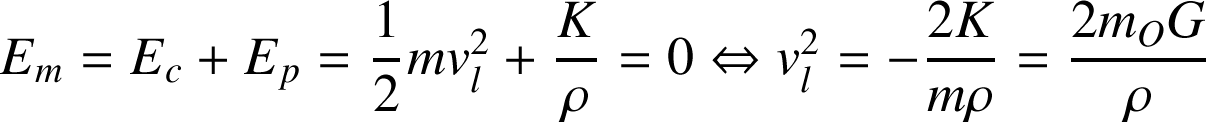
Exemple :
La Terre décrit une orbite autour du Soleil : en moyenne
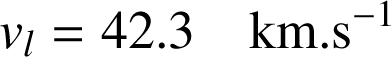, valeur supérieure à
.
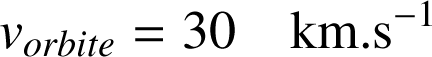Exemple :
Le Soleil serait un trou noir si
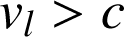, soit pour
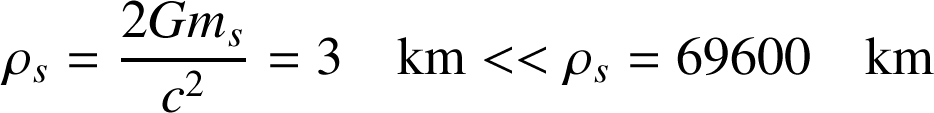
Exemple :
Mouvement d'un Satellite (S) autour de la Terre (T)
Les satellites décrivent généralement un mouvement circulaire uniforme autour de la Terre. Leur trajectoire se fait toujours dans un plan qui passe par le centre de la Terre puisque la force d'attraction gravitationnelle est une force centrale. Soit
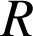la distance séparant S du centre de la Terre. Le PFD nous dit que :
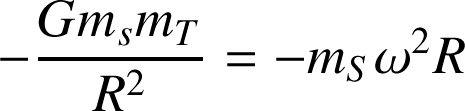
Avec
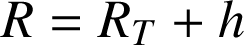où
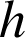est l'altitude du satellite et
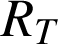le rayon de la Terre.
Cette relation nous permet de retrouver la troisième loi de Kepler :
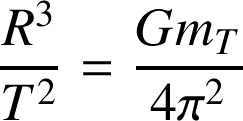
Définition :
La vitesse de satellisation
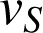pour un mouvement circulaire uniforme est obtenue en écrivant le PFD sous la forme suivante :
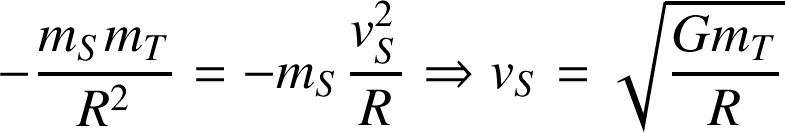
Exemple :
Pour le satellite SPOT situé à une altitude
.
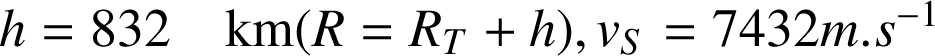Relation entre
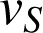et
:
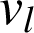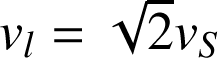
Satellite géostationnaire : S a une position fixe par rapport au référentiel terrestre R' en rotation. Cela signifie que la vitesse relative de S est nulle, donc :
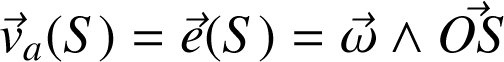
Le mouvement d'entraînement de S sera donc dans la direction perpendiculaire à celle du vecteur rotation. De plus, on sait déjà que la trajectoire d'un satellite se fait dans un plan passant par le centre de la Terre. Pour satisfaire ces deux conditions, S doit nécessairement se trouver dans le plan équatorial. De plus le PFD avec
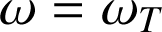donne le rayon de l'orbite géostationnaire :
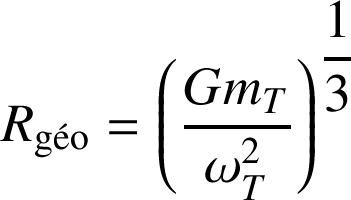
A. N. :
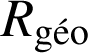= 42000 km, soit
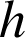= 36000 km.
Energie de satellisation pour un mouvement circulaire uniforme
:
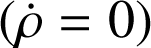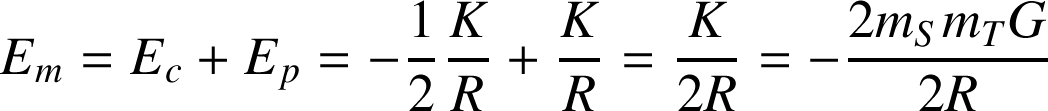
On observe que
.
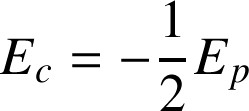Note. Comme la Terre tourne sur elle-même, le lancement du satellite se fera préférentiellement à l'équateur, de sorte à bénéficier au maximum de la vitesse d'entraînement (section 3.5).
