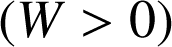On cherche à caractériser l'action d'une force
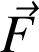appliquée à un point
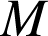en mouvement.
Définition :
Dans le référentiel R, le travail élémentaire
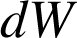d'une force
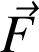pendant un temps
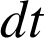vaut :
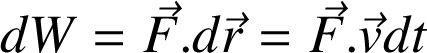
En coordonnées cartésiennes, le produit scalaire
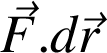s'écrit :
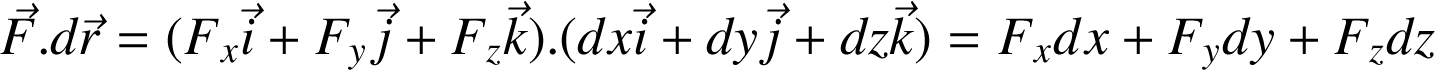
Définition :
Sur un trajet fini,
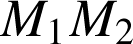, le travail
vaut :
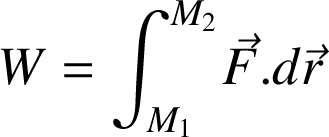
Cette équation est appelée intégrale curviligne car prise le long d'une courbe. Le schéma qui suit présente le cas particulier d'une force
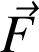constante (p. ex. le poids) qui s'applique à un point matériel
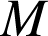qui décrit une trajectoire entre les points
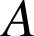et
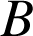. Le vecteur
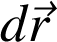est, en tout point, tangent à la trajectoire :
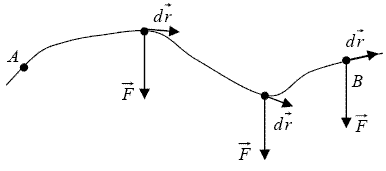
Le travail
est un scalaire qui représente la circulation de
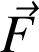sur la courbe
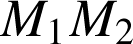. Unité de
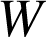: le Joule (J) = kg.m2.s-2.
Définition :
Le travail est : soit résistant (W < 0), soit nul (p. ex. si
|  Illustration de travaux moteur résistants ou nuls |
Exemple :
Cas particulier. Le travail
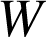d'une force
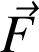constante, sur une trajectoire rectiligne représentée par le vecteur
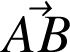vaut :
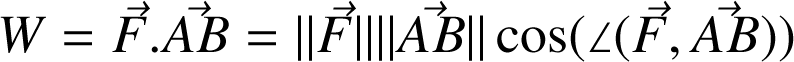
Exemple :
Le travail du poids
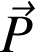sur une masse
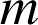se déplaçant dans l'espace
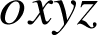du point A au point B (axe
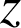orienté vers le haut) vaut :
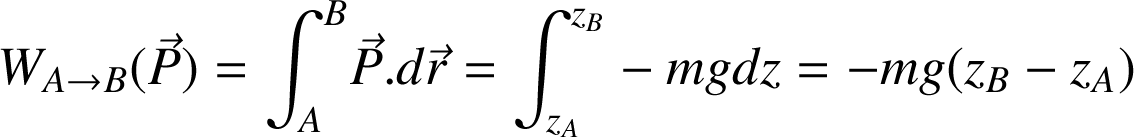
Si
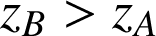, le travail est résistant ; dans le cas contraire
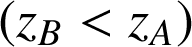il est moteur. Le travail du poids dépend de la différence des hauteurs, et pas des coordonnées x et y, on dira que le travail est indépendant du chemin suivi.
Exemple :
Le travail associé à la force de rappel
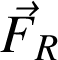de l'extrémité d'un ressort horizontal :
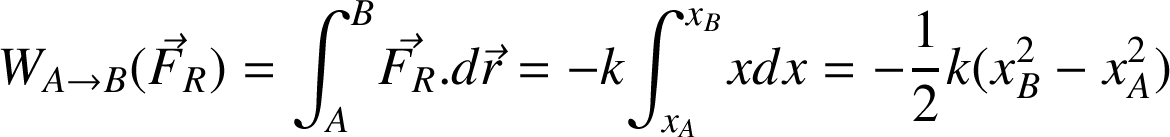
Lorsque le déplacement s'effectue vers le point d'équilibre (p. ex.
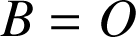), dans le sens de
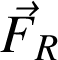, le travail est moteur ; dans le cas contraire (p. ex.
), il est résistant.
Exemple :
Le travail d'une force Newtonienne du type
:
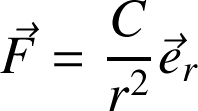Pour illustrer l'utilisation d'un système de coordonnées non cartésiennes, plaçons nous dans un plan et travaillons en coordonnées polaires. Le vecteur de déplacement infinitésimal s'écrit (section 2.2) :
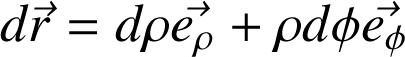
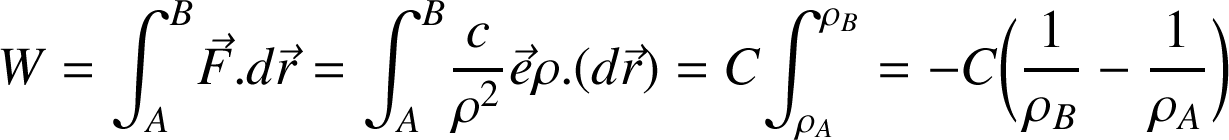
Force gravitationnelle :
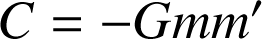. Supposons que l'origine des coordonnées se situe en
. Considérons la force gravitationnelle qu'exerce
sur
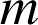. Lorsque
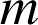se déplace du point
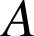au point
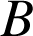, le travail sera moteur si
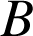se rapproche de l'origine (de
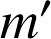) ; il sera résistant si le point
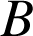s'en éloigne. Sur Terre, il est courant d'utiliser l'expression du poids plutôt que de la force gravitationnelle pour exprimer les effets de la gravitation. En posant
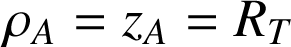et
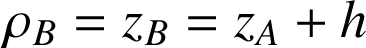dans l'expression de
, on retrouve le résultat obtenu dans l'exemple ii) à condition de supposer
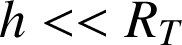. Cet exemple a donc un caractère plus général.
Force électrostatique :
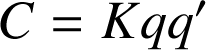. Il faut distinguer le cas où les charges ont mêmes signes de celui où elles ont un signe opposé. Le travail associé au rapprochement de charges de signes contraire est moteur, celui associé à leur éloignement est résistant. Le contraire s'applique à deux charges de mêmes signes.
Définition :
Forces conservatives
Une force
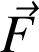est dite conservative si :
elle ne dépend que de la position de l'objet (et pas de
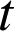) ;le travail qui lui est associé lorsque M se déplace entre deux positions quelconques ne dépend que des positions initiale et finale (et pas du parcours suivi).
Une conséquence du 2ème point est que la circulation sur un chemin fermé de
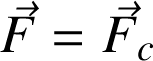(l'indice c indique que la force est conservative) est nulle :
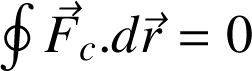
Exemple :
Le travail du poids
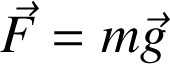(exemple ii)) ne dépend pas du chemin suivi mais uniquement des bornes (ici
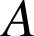et
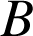). Si le travail est calculé sur un chemin fermé, alors
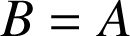et
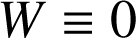. Le poids est donc une force conservative, au même titre que les forces newtonienne ou que la force de rappel d'un ressort.
Définition :
Forces dissipatives
Les forces dissipatives sont des forces non conservatives qui transforment l'énergie mécanique en énergie thermique au cours du temps (cours de thermodynamique en L2 et L3).
Exemple :
La force de frottement. En l'absence d'une expression analytique de cette force, on le voit bien sur le schéma ci-dessous : la force de frottement, toujours opposée au sens du mouvement, change de signe selon le trajet
ou le trajet
. Les contributions vont donc s'additionner au lieu de se soustraire, comme pour les forces conservatives.
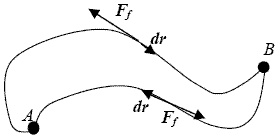
Ainsi pour une trajectoire rectiligne de longueur L :
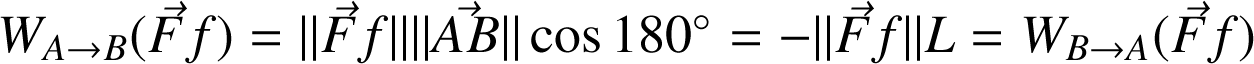
Soit
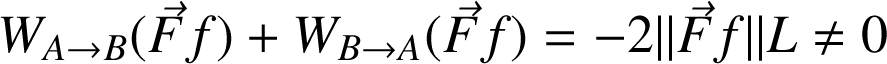
Définition :
Puissance d'une force
La puissance P de la force
est définie par :
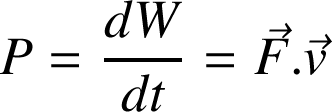
La puissance s'exprime en Watt (W) = 1 kg.m2.s-3.
