Complément :
Pré-requis mathématique
Le vecteur gradient de la fonction scalaire
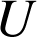, noté
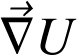(ou
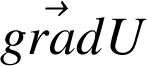) est défini par :
Base cartésienne :
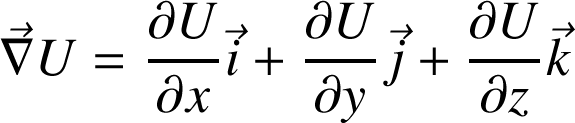
Base cylindrique :
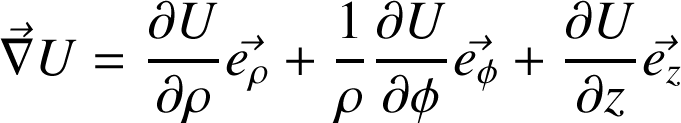
Base sphérique :
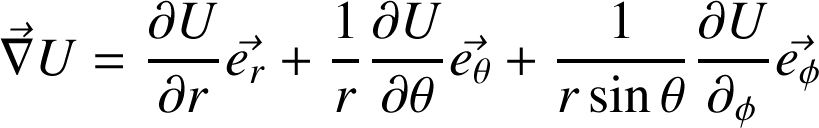
Il exprime le taux de variation de
dans chacune des trois directions indiquées par les vecteurs de base. Le vecteur gradient est dirigé vers la plus haute valeur de
.
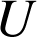Définition :
Potentiel : si un vecteur
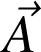satisfait la relation
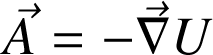
alors la fonction
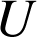est appelée potentiel de
.
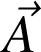Définition :
On appelle équipotentielle la courbe (ou la surface dans un espace à trois dimensions) qui relie les points de
qui ont même valeur. Le vecteur gradient de
appliqué en un point de cette courbe lui est toujours perpendiculaire (et dirigé vers l'équipotentielle plus élevée).
Exemple :
Cherchons la fonction potentiel
associé au poids
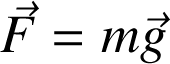d'un corps de masse
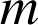. Soit
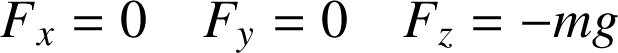. Avec l'axe z orienté vers le haut, on obtient :
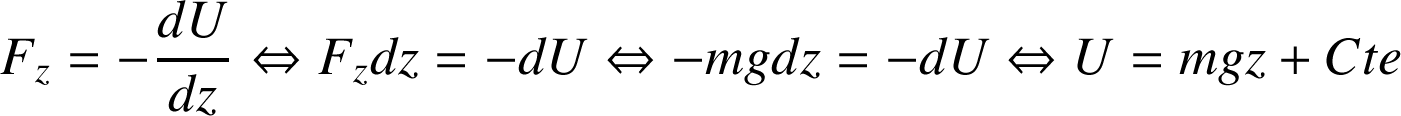
Remarque :
On remarque que toute fonction potentiel scalaire
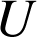associée à une force a la dimension d'une énergie, d'où l'appellation d'énergie potentielle :
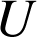sera alors notée
.
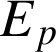La fonction potentiel, ou énergie potentielle, associée au poids est :
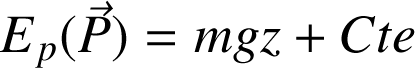
Il est d'usage de poser
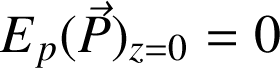, de sorte à ce que la constante soit nulle.
Exemple :
L'énergie potentielle associée à la force de rappel
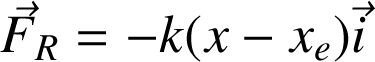d'un ressort horizontal vaudra :
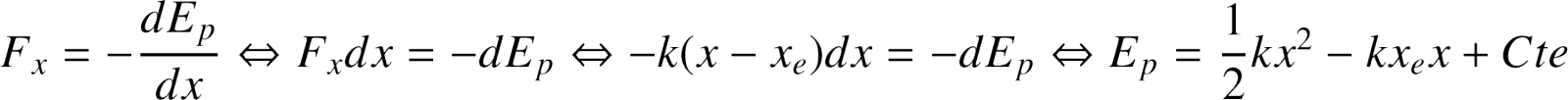
Il est d'usage de poser
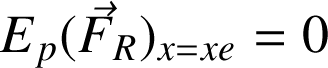car la force de rappel du ressort est nulle à l'équilibre. Dans ce cas,
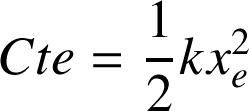et l'énergie potentielle associée à la force de rappel d'un ressort vaut :
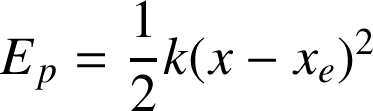
Exemple :
L'énergie potentielle associée à une force newtonienne
:
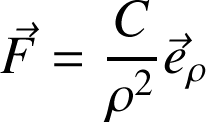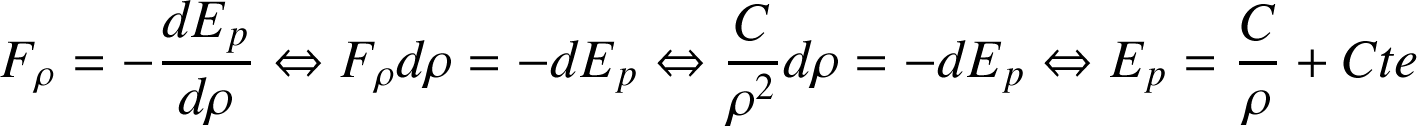
Ce qui se résume par :
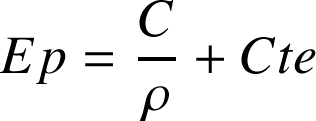
A nouveau on fait un choix arbitraire pour déterminer la valeur de la constante d'intégration. Dans le cas d'une force newtonienne, l'interaction devient négligeable a grande distance. Il est donc d'usage de poser
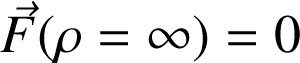, ce qui implique
.
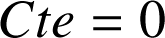Fondamental :
Propriétés d'une force conservative
Les quelques exemples illustrent le fait que toute force conservative
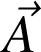possède un potentiel scalaire
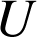(une energie potentielle) qui satisfait la relation
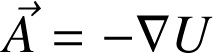. Inversement, chaque potentiel scalaire sera associé a un vecteur (force) conservatif. Par ailleurs, il n'y a pas d'énergie potentielle "absolue" en raison de la présence de la constante d'intégrations. Cela n'est pas gênant car, en physique, seules des différences d'énergies potentielles peuvent être mesurées.
Ces propriétés ont une conséquence importante en mécanique du point matériel.
Enoncé : La variation de l'énergie potentielle
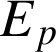est égale et de signe opposé au travail
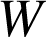de la force conservative
.
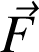En effet, on peut montrer en mathématique que (
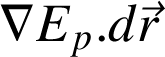est une différentielle totale de
) :
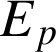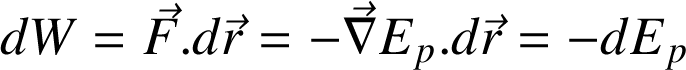
Nous retiendrons :
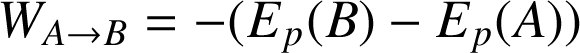
Fondamental :
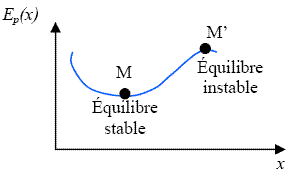
Equilibre d'un point et notion de stabilité (voir schéma)
L'étude de la fonction analytique énergie potentielle permet de caractériser les positions de stabilité d'un système. Pour simplifier, on traite un problème à une dimension, par exemple selon
:
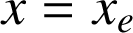est une position d'équilibre si
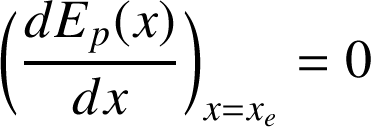;L'équilibre est stable (minimum) si
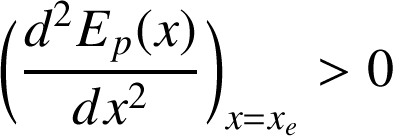;L'équilibre est instable (maximum) si
;
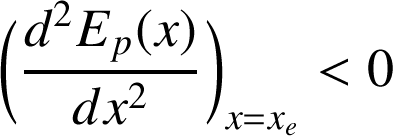