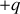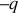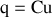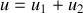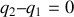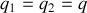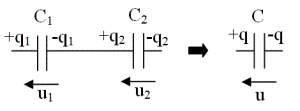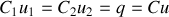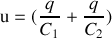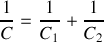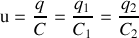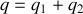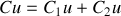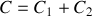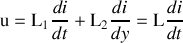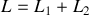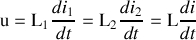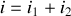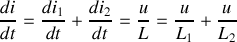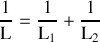Condensateur
Définition :
En théorie, un condensateur plan est constitué de deux plaques métalliques de forme quelconque, appelées armatures, séparées par un milieu isolant appelé diélectrique. Lorsque le condensateur est chargé, l'une des armatures porte la charge
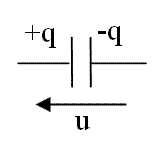|  condensateur |
Le coefficient
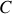est appelé capacité du condensateur et s'exprime en Farads (F).
Comme
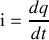, on en déduit que
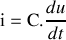. : équation différentielle linéaire à coefficient constant qui constitue l'équation caractéristique du condensateur.
→ En régime continu,
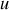= constante, donc
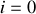: le condensateur se comporte comme un interrupteur ouvert et empêche le passage du courant dans le circuit.
Remarque :
L'isolant n'étant pas parfait, on considère parfois que le condensateur « réel » est constitué d'un condensateur « parfait » monté en parallèle avec une résistance très grande
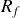appelée résistance de fuite.
Lois d'associations
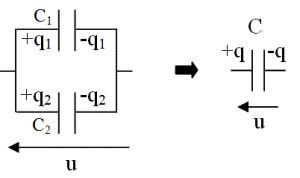
en série
Dans le schéma ci-contre,
|  condensateurs en série |
On en tire
, soit
et donc
en parallèle
Dans le schéma ci-contre,
Comme il faut que
|  condensateurs en parallèle |
Puissance
En régime permanent continu, P = 0.
De même que pour la résistance, il ne faut pas dépasser une valeur maximale de la tension prescrite par le constructeur sous peine de destruction du composant.
La relation
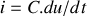impose que la tension aux bornes d'un condensateur ne peut pas subir de discontinuité, car le courant et donc la puissance seraient infinis.
Self ou «bobine»
Définition :
Il s'agit d'un enroulement de conducteur sous forme de spires. Traversée par un courant variable, elle est le siège de phénomènes d'auto-induction créant une tension entre ses bornes :
équation différentielle à coefficient constant qui constitue l'équation caractéristique de la self. Le coefficient L est appelé inductance de la bobine et se mesure en Henrys (H). | 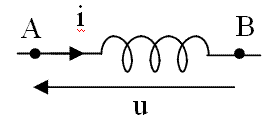 bobine |
Remarque :
Comme le condensateur, la self pure n'existe pas : le fil conducteur dont elle est formée possède toujours une résistance r, et entre les spires, il subsiste une très faible capacité C. Le schéma réel est donc une inductance pure L, avec une résistance r en série, le tout en dérivation avec un condensateur de capacité C. Les valeurs de r et C dépendent de la fréquence du signal. L'effet de la capacité n'apparaît qu'aux très hautes fréquences.
→ Si l'on néglige cette capacité, l'équation caractéristique d'une bobine réelle s'écrit
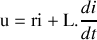
En régime continu, la dérivée est nulle et cette bobine se réduit à un fil de résistance r.
Lois d'associations
en série
Dans le schéma ci-contre,
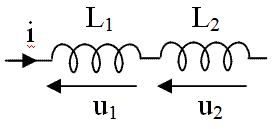|  bobines en série |
en parallèle
dans le schéma ci-contre,
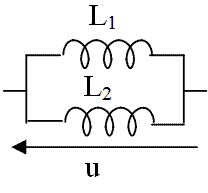|  bobines en parallèle |
Puissance
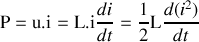En régime permanent, P = 0.
La relation
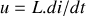impose que le courant traversant une bobine ne peut pas subir de discontinuité, car la tension à ses bornes, et donc la puissance, seraient infinis.
