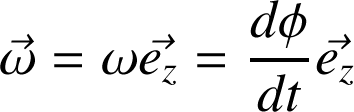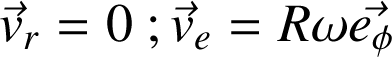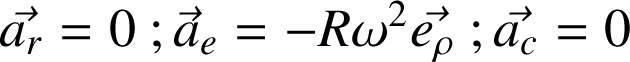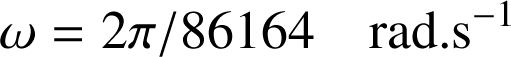Un point M sur une roue de vélo qui avance ...
Définition :
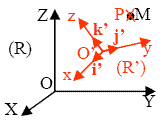 definitions | (R) : référentiel fixe ou absolu (R') : référentiel mobile ou relatif ( i', j', k' ) : base orthonormée liée à (R') P : point coïncidant. Point fixe de (R') qui coïncide, à l'instant t, avec le point mobile M. Hypothèse : le temps est absolu (t = t') (acceptable si v << c) |
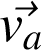: vitesse absolue. Vitesse du point M dans le référentiel absolu (R).
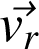: vitesse relative. Vitesse du point M dans le référentiel relatif (R').
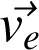: vitesse d'entraînement. Vitesse du point coïncidant P dans le référentiel absolu (R).
Les mêmes définitions s'appliquent à l'accélération.
Fondamental : Loi de transformation des vitesses
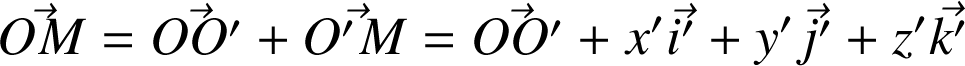
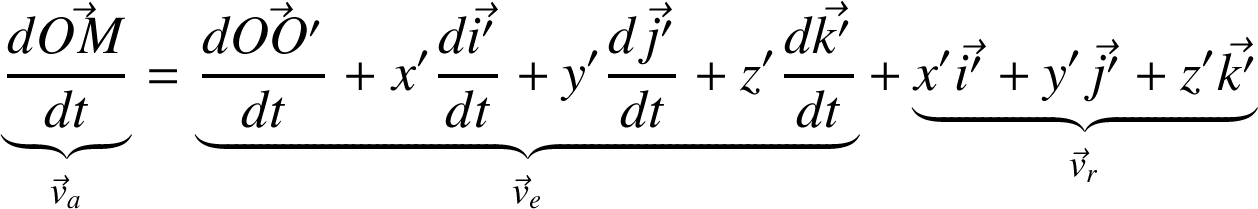
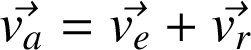
De par la définition du vecteur rotation
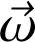, on peut exprimer
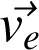comme :
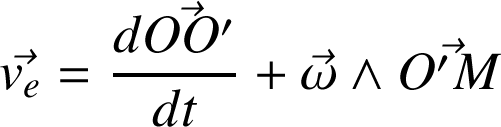
En particulier le second terme de la vitesse d'entraînement ne diffère de zéro que si le référentiel (R') effectue une rotation par rapport à (R)
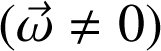dans laquelle
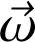n'est pas parallèle à
.
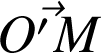Fondamental : Loi de transformation des accélérations
Définition :
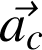est appelée accélération de Coriolis.
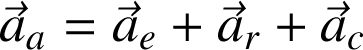
On peut également exprimer les vecteurs accélération d'entraînement et de Coriolis en fonction du vecteur rotation
:
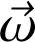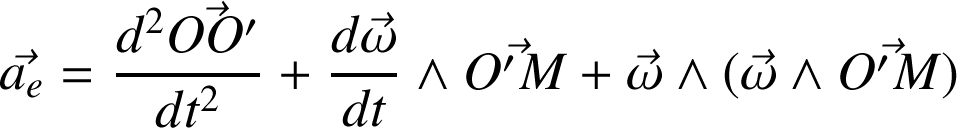
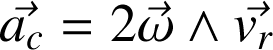
En particulier l'accélération de Coriolis ne diffère de zéro que si le référentiel (R') effectue une rotation par rapport à (R)
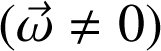dans laquelle
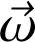n'est pas parallèle à
.
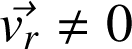Fondamental :
Application : le mouvement relatif de (R') par rapport à (R) est une translation
Cela signifie que la direction des vecteurs de base
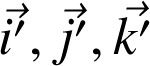est fixe par rapport à (R) :
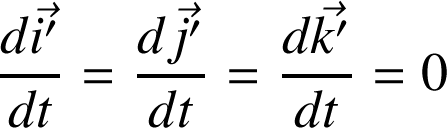
Note : en gardant l'orientation du trièdre fixe, le mouvement de O' peut ne pas être rectiligne.
La vitesse d'entraînement est la même pour tous les points de (R') :
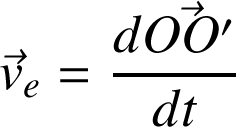
L'accélération d'entraînement est la même pour tous les points de (R') :
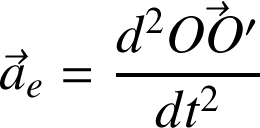
Enfin, l'accélération de Coriolis est nulle pour tout point de (R').
Exemple :
Traitons un exemple. Un voyageur laisse tomber un objet M dans un train qui se déplace à vitesse constante
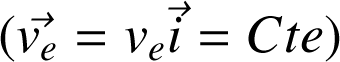. Quelle est la trajectoire de l'objet M pour le voyageur (R'), et pour l'observateur situé le long de la voie (R) ?
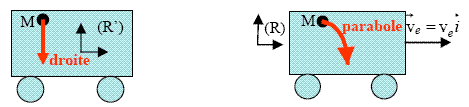
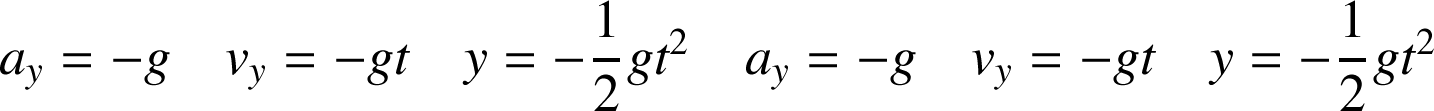
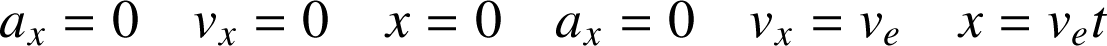
Fondamental : Application : le mouvement relatif de (R') par rapport à (R) est une
Pour simplifier le problème, on suppose que la rotation s'effectue autour de l'axe oz (voir schéma).
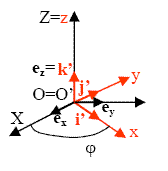
La vitesse d'entraînement est donnée par l'expression :
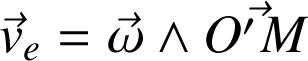
L'accélération d'entraînement est donnée par l'expression :
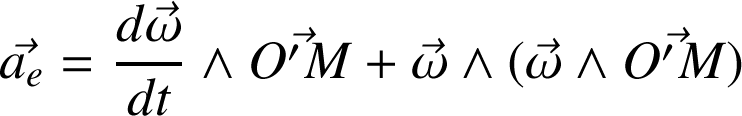
Enfin la relation qui donne l'accélération de Coriolis est :
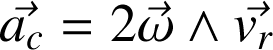
Remarque : Cas général
Un mouvement quelconque se décompose toujours en un mouvement de translation et un mouvement de rotation (additionner les termes avec O et O' distincts).
Exemple : a) Exemple du cygne sur un manège (R')
 manège | Pour le cygne sur le manège :
|
Exemple : b) Exemple du lancement de satellite
La Terre (R') est en rotation sur elle-même, le vecteur rotation est dirigé approximativement selon un axe Nord-Sud. Pour un observateur placé dans un référentiel (R) attaché par exemple au système solaire, (R') est animé d'un mouvement de rotation et de translation :
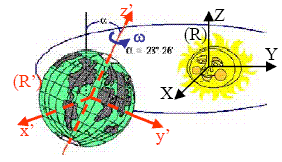 rotation de la terre autour du soleil | La Terre tourne autour du Soleil : O' est en par rapport à O La Terre sur elle-même : axe de rotation z' avec
|
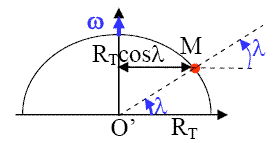
Soit M un satellite situé à la surface de la Terre à une latitude
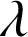. La vitesse absolue de lancement de M sera maximale si la vitesse d'entraînement est aussi maximale :
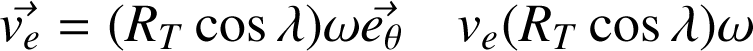
Cela sera le cas à l'équateur,
.
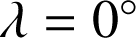Résoudre le problème décrit dans la motivation de ce chapitre. Pour cela décrire le mouvement d'un point M situé sur une roue de vélo dans le référentiel (R'), puis dans le référentiel (R), à l'aide des relations obtenues ci-dessus. Note : (R') effectue un mouvement de translation par rapport à (R) dans la direction horizontale.
