L'accélération est une grandeur (unité : m.s-2) qui exprime le rapport de la distance parcourue au carré la durée mise pour la parcourir. C'est aussi une mesure de la variation de la vitesse par unité de temps.
Définition : Accélération moyenne
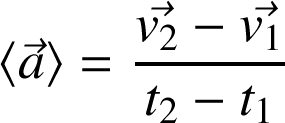

Définition : Accélération instantanée
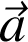 : c'est la limite de l'accélération moyenne lorsque la durée tend vers zéro. Dans un référentiel R donné,
: c'est la limite de l'accélération moyenne lorsque la durée tend vers zéro. Dans un référentiel R donné,
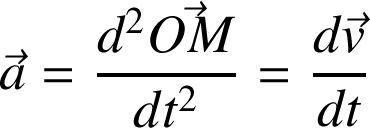
Définition : Exemple dans une base fixe, en coordonnées cartésiennes (suite) :
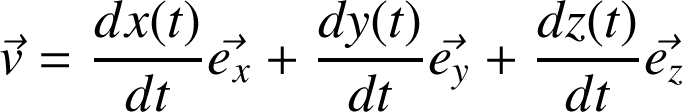
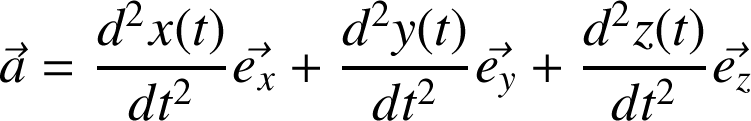
Définition : Exemple dans la base locale cylindrique
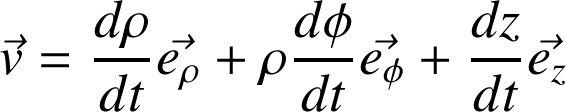
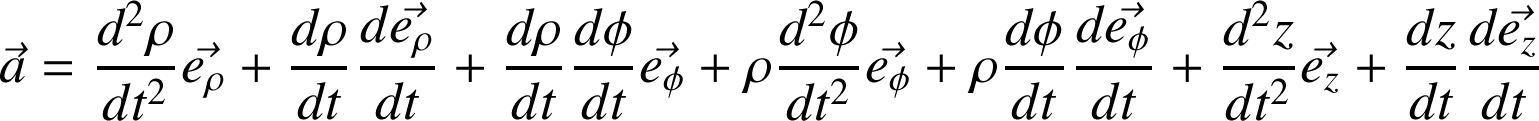
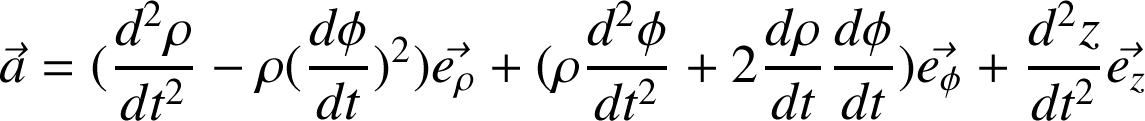
Définition :
Dans la base locale des coordonnées polaires, l'expression se réduit à :
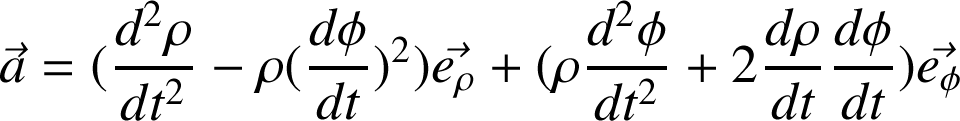
Fondamental :
De manière générale l'orientation du vecteur accélération instantanée au point M de la courbe est établie dans la base de Serret-Frenet (coordonnées intrinsèques) :
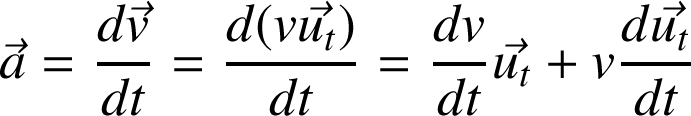
Par ailleurs,
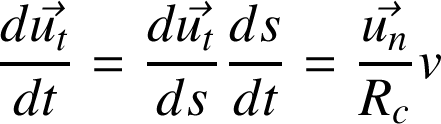
On obtient une expression générale du vecteur accélération :
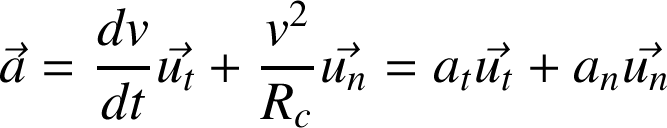
Le vecteur accélération a deux composantes (
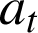 et
et
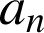 ). On distingue deux grandes catégories de mouvement :
). On distingue deux grandes catégories de mouvement :
Définition :
1) Les mouvements rectilignes (1D) : le rayon de courbure est infini,
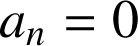 . Les vecteurs
. Les vecteurs
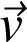 et
et
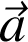 sont portés par un axe, soit ox. Le mouvement est accéléré (retardé) si
sont portés par un axe, soit ox. Le mouvement est accéléré (retardé) si
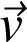 et
et
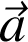 ont mêmes sens (sens opposés).
ont mêmes sens (sens opposés).
Définition :
2) Les mouvements uniformes : la norme de la vitesse est constante,
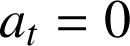 .
.
Remarque :
Pour la suite il faut apprendre à obtenir
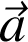 connaissant
connaissant
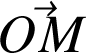 ou
ou
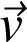 :
:
Dans un repère fixe oxyz : en coordonnées cartésiennes
Dans les bases locales des coordonnées cylindriques, polaires, intrinsèques



