On peut maintenant étudier la cinématique du point matériel M par rapport à un référentiel R fixe, lié à l'observateur.
Le système de coordonnées doit être le plus judicieusement choisi.
Mouvement rectiligne
Fondamental :
L'hypothèse du mouvement rectiligne est remplie en imposant que le vecteur vitesse initiale
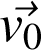 soit dans la même direction que le vecteur accélération (ici la direction
soit dans la même direction que le vecteur accélération (ici la direction
 ). On traitera en particulier le mouvement rectiligne uniforme
). On traitera en particulier le mouvement rectiligne uniforme
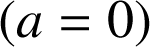 et le mouvement rectiligne uniformément accéléré (varié) où l'accélération est constante
et le mouvement rectiligne uniformément accéléré (varié) où l'accélération est constante
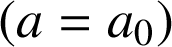 . Les équations du mouvement sont les suivantes :
. Les équations du mouvement sont les suivantes :
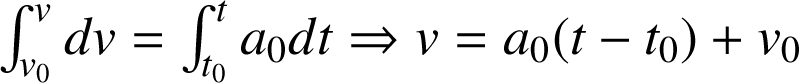
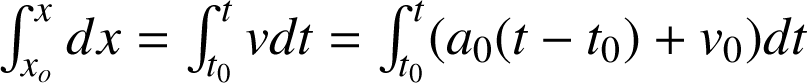
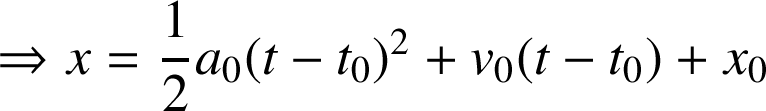
Mouvement uniformément accéléré (mouvement parabolique)
Fondamental :
Il s'agit de reprendre les équations ci-dessus dans un cas général, à savoir
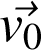 et
et
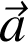 peuvent avoir des directions différentes :
peuvent avoir des directions différentes :

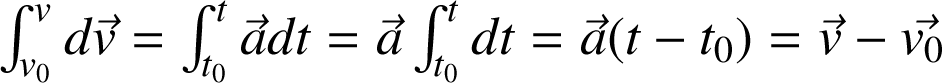
soit
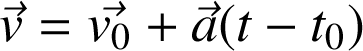
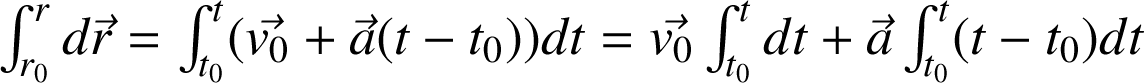
soit
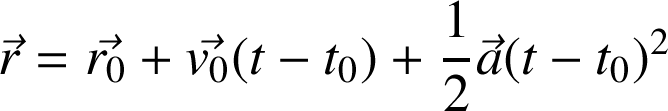
Exemple : Mouvement d'un projectile dans un plan sous l'action de la pesanteur

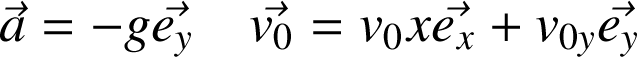
L'expression de
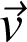 , avec
, avec
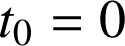 nous donne
nous donne
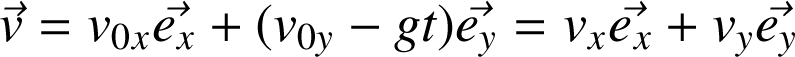
Cette relation indique que seule la composante de la vitesse dirigée selon
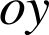 varie en fonction du temps. Si on prend l'origine du référentiel en
varie en fonction du temps. Si on prend l'origine du référentiel en
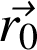 , l'équation de la trajectoire
, l'équation de la trajectoire
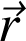 s'écrit :
s'écrit :
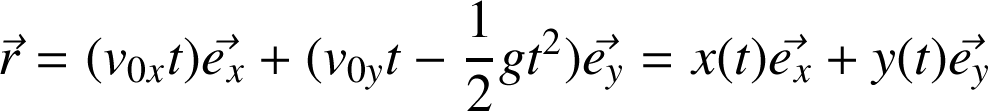
Une fois les équations établies, on peut analyser le mouvement. Ainsi, le temps nécessaire pour atteindre le sommet A de la trajectoire est obtenu en posant
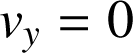 dans l'expression de
dans l'expression de
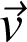 . Alors :
. Alors :
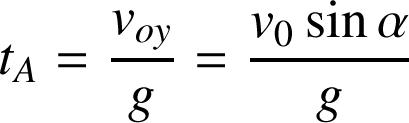
Au temps
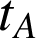 , on peut obtenir l'expression analytique de la hauteur maximale
, on peut obtenir l'expression analytique de la hauteur maximale
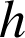 en calculant
en calculant
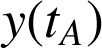 grâce à l'expression de
grâce à l'expression de
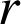 :
:
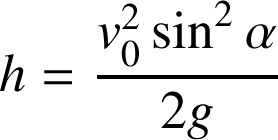
Le temps de vol du projectile, c'est-à-dire la durée qu'il faut pour que le projectile arrive au sol au point B, s'obtient en posant
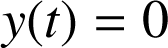 dans l'expression de
dans l'expression de
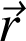 :
:
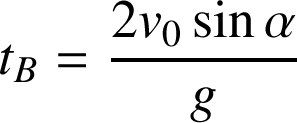
La portée est la distance OB, elle est obtenue en calculant
 dans l'expression de
dans l'expression de
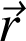 :
:
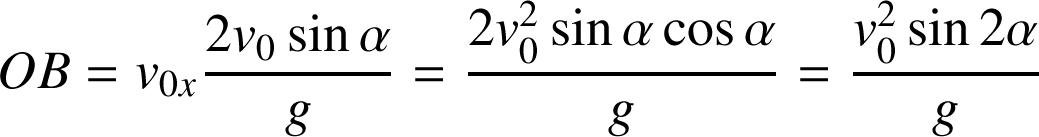
La portée est maximale pour
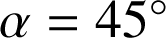 .
.
Enfin, l'équation de la trajectoire est obtenue en éliminant
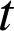 dans
dans
 et
et
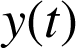 :
:
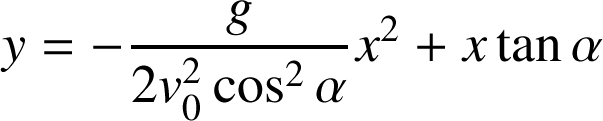
C'est l'équation d'une parabole.
Mouvement circulaire (uniforme et non-uniforme)
Fondamental :
La trajectoire est un cercle. Mouvement décrit naturellement en coordonnées polaires. Le rayon
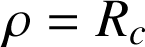 est une constante (indépendante de
est une constante (indépendante de
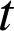 ), l'angle
), l'angle
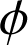 est une fonction de la variable
est une fonction de la variable
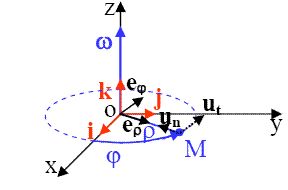
 . En coordonnées cylindriques, oz est l'axe de rotation (voir schéma).
. En coordonnées cylindriques, oz est l'axe de rotation (voir schéma).
a) mouvement circulaire non-uniforme (cas général) :
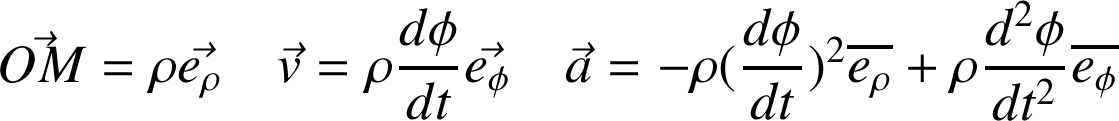
On introduit le vecteur rotation
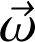 , dirigé dans l'exemple selon oz :
, dirigé dans l'exemple selon oz :
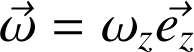
On a vu que
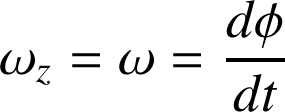 . Les vecteurs
. Les vecteurs
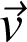 et
et
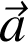 peuvent être réécrits :
peuvent être réécrits :

Ou bien encore :
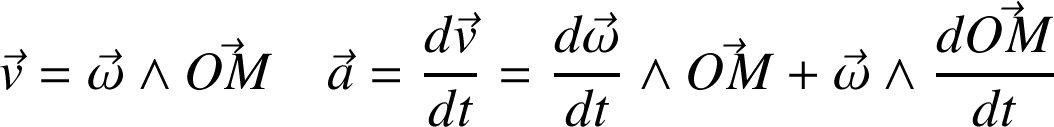
b) mouvement circulaire uniforme :
La vitesse est constante. Comme
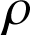 est constant, on obtient
est constant, on obtient
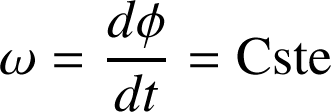 . Donc,
. Donc,
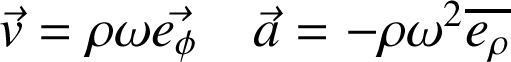
L'accélération est dirigée vers le centre du cercle et on vérifie qu'elle est égale à
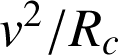 .
.
Mouvement à accélération centrale
Définition :
Mouvement d'un point M tel qu'à chaque instant le vecteur accélération
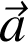 passe par un point fixe appelé O. Mouvement possédant des propriétés remarquables. Mathématiquement :
passe par un point fixe appelé O. Mouvement possédant des propriétés remarquables. Mathématiquement :
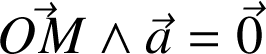 car
car
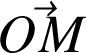 et
et
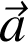 sont des vecteurs parallèles.
sont des vecteurs parallèles.
Définition : Loi des aires
On définit le vecteur « vitesse aréolaire »
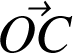 par la relation :
par la relation :
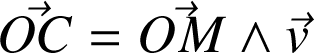
Fondamental :
Le vecteur
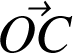 est une constante du mouvement (il n'est pas fonction du temps) :
est une constante du mouvement (il n'est pas fonction du temps) :
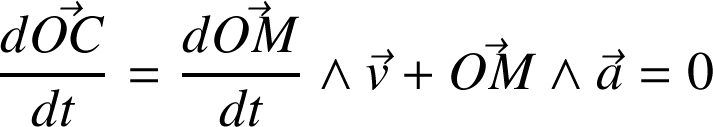 (cqfd)
(cqfd)
Comme
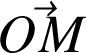 est perpendiculaire à
est perpendiculaire à
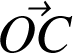 qui possède une direction fixe,
qui possède une direction fixe,
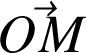 décrit nécessairement une trajectoire plane (voir schéma).
décrit nécessairement une trajectoire plane (voir schéma).
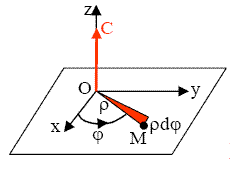
Le système de coordonnées cylindriques dans sa base mobile est approprié à la description du mouvement :
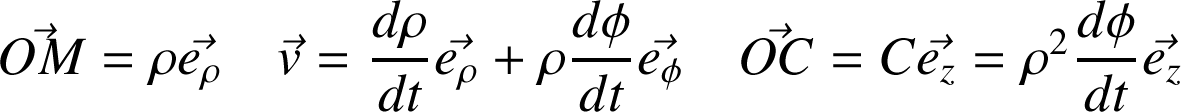
Le module C est lié à l'élément de surface élémentaire
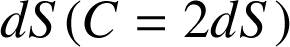 balayé par le vecteur
balayé par le vecteur
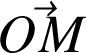 (voir schéma) en un temps
(voir schéma) en un temps
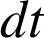 . C est constant.
. C est constant.
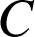 est la constante de la loi des aires « la surface balayée par unité de temps est constante » :
est la constante de la loi des aires « la surface balayée par unité de temps est constante » :
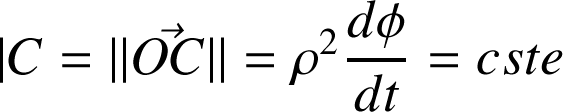
Application : le mouvement des planètes.



