La vitesse est une grandeur (unité : m.s-1) qui exprime le rapport de la distance parcourue à la durée mise pour la parcourir.
Le vecteur vitesse
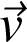 contient comme information la direction et le sens du mouvement ; sa norme est la vitesse scalaire. On définit les vecteurs vitesse moyenne et vitesse instantanée.
contient comme information la direction et le sens du mouvement ; sa norme est la vitesse scalaire. On définit les vecteurs vitesse moyenne et vitesse instantanée.
Définition :
Vitesse moyenne :
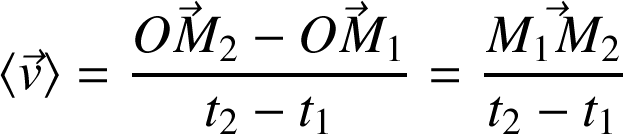
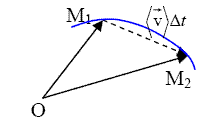
Définition :
Vitesse instantanée :
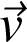 c'est la limite de la vitesse moyenne lorsque la durée tend vers zéro. Dans un référentiel
c'est la limite de la vitesse moyenne lorsque la durée tend vers zéro. Dans un référentiel
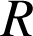 donné,
donné,
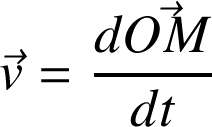
Par sa définition, le vecteur vitesse instantanée est tangent à la trajectoire au point
 (section 2.4).
(section 2.4).
Définition : Dans la base de Serret-Frenet
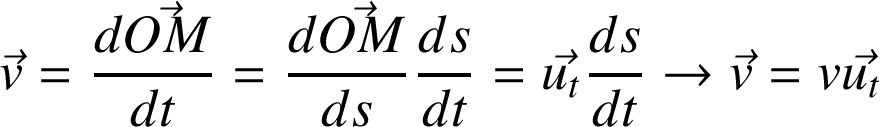 avec la vitesse scalaire :
avec la vitesse scalaire :
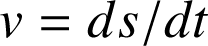
Méthode :
Le problème généralement posé à un observateur, situé dans un référentiel
 , est d'obtenir le vecteur vitesse instantanée du point
, est d'obtenir le vecteur vitesse instantanée du point
 . On procède comme suit.
. On procède comme suit.
a) Lorsque le vecteur
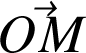 est repéré dans une base fixe (par rapport à
est repéré dans une base fixe (par rapport à
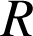 ) oxyz : calculer les composantes du vecteur vitesse en dérivant les composantes correspondantes du vecteur position par rapport au temps.
) oxyz : calculer les composantes du vecteur vitesse en dérivant les composantes correspondantes du vecteur position par rapport au temps.
Exemple :
Exemple en coordonnées cartésiennes :
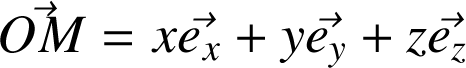
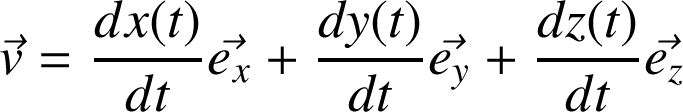
Méthode :
b) Lorsque le vecteur
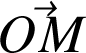 est repéré dans une base mobile (par rapport à
est repéré dans une base mobile (par rapport à
 et oxyz) : dériver par rapport au temps à la fois les composantes du vecteur position et les vecteurs unitaires de la base mobile.
et oxyz) : dériver par rapport au temps à la fois les composantes du vecteur position et les vecteurs unitaires de la base mobile.
Exemple :
Exemple dans la base locale cylindrique.
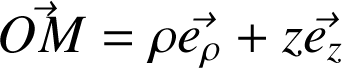
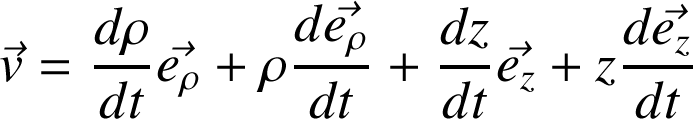
Notons d'abord que
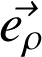 et
et
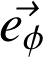 dépendent du temps (ces vecteurs tournent avec le point M), mais pas
dépendent du temps (ces vecteurs tournent avec le point M), mais pas
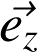 . En faisant usage des relations de la section 2.2, on a :
. En faisant usage des relations de la section 2.2, on a :
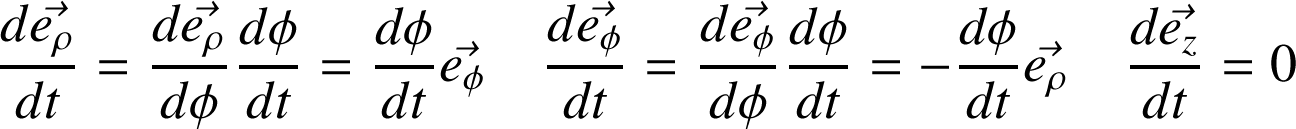
On obtient
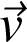 :
:
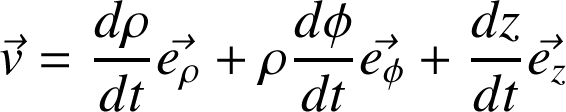
Méthode :
Dans la base locale des coordonnées polaires (2D), seuls les deux premiers termes subsistent ; les composantes associées à
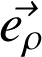 et
et
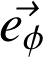 sont appelées composantes radiale et orthoradiale, respectivement.
sont appelées composantes radiale et orthoradiale, respectivement.
Remarque :
Pour la suite il faut apprendre à obtenir
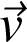 connaissant
connaissant
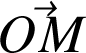 :
:
Dans un repère fixe oxyz : en coordonnées cartésiennes
Dans les bases locales des coordonnées cylindriques, polaires, intrinsèques
Définition : Vitesse instantanée de rotation
On introduit d'abord le vecteur rotation
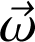 . Par définition, dans une base mobile formée de trois vecteurs unitaires orthonormés
. Par définition, dans une base mobile formée de trois vecteurs unitaires orthonormés
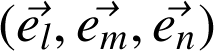 ,
,
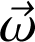 satisfait les relations suivantes :
satisfait les relations suivantes :
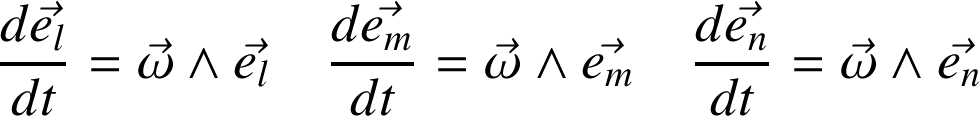
Par exemple, dans la base mobile
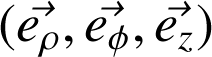 , on peut voir que
, on peut voir que
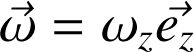 satisfait les trois conditions ci-dessus et que de plus ces relations conduisent à
satisfait les trois conditions ci-dessus et que de plus ces relations conduisent à
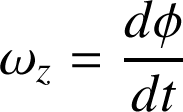 ; il s'agit d'une vitesse angulaire (rad.s-1) que l'on désigne comme vitesse instantanée de rotation, et qui est souvent notée
; il s'agit d'une vitesse angulaire (rad.s-1) que l'on désigne comme vitesse instantanée de rotation, et qui est souvent notée
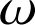 au lieu de
au lieu de
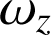 . Application : mouvement circulaire uniforme (section 3.4).
. Application : mouvement circulaire uniforme (section 3.4).



