Soit 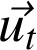le vecteur unitaire tangent à la courbe au point 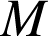, et soit 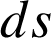l'élément de longueur duquel 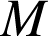se déplace le long de la courbe pour aller en :

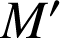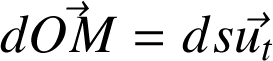
Abscisse curviligne

Donc,

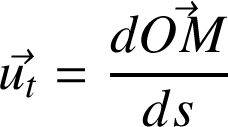
On exprime 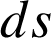grâce à la définition de la norme de :

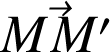1. en coordonnées cartésiennes :

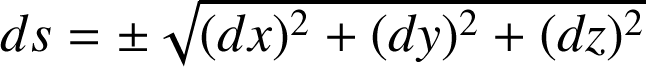
2. en coordonnées cylindriques :

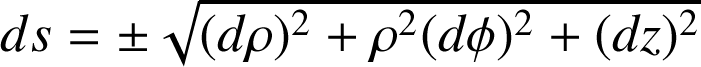
3. en coordonnées sphériques :

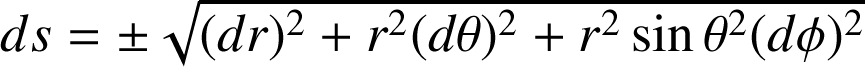
Par intégration de on obtient , qui est appelée abscisse curviligne.

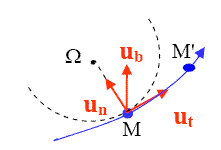
Dans la base de Serret-Frenet des coordonnées intrinsèques, on peut démontrer, à l'aide du schéma et de l'approximation des petits angles, que :

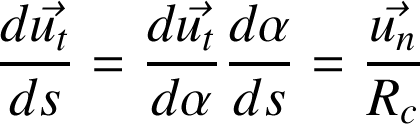
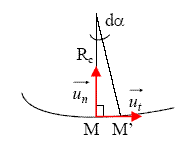
base de Serret-Frenet