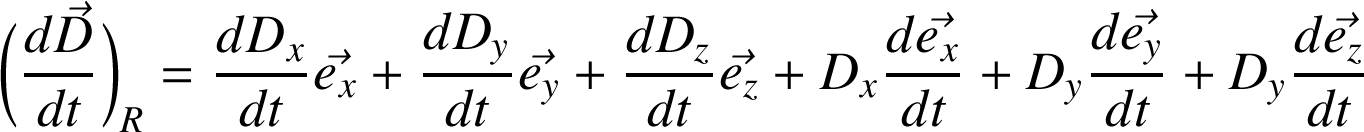Définition :
On appelle dérivée du vecteur
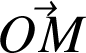par rapport à la variable
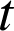, en
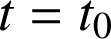, le vecteur :
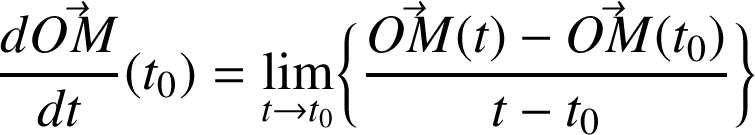
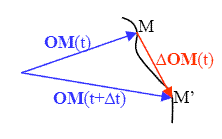
Interprétation géométrique : la dérivée de
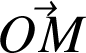est un vecteur dirigé selon la tangente en
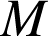à la courbe (lorsque
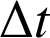diminue,
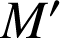se rapproche de
,
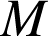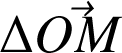devient tangent).
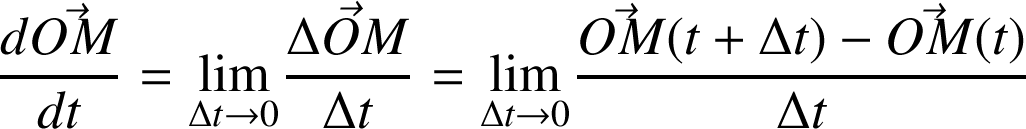
Définition :
Dans un référentiel
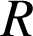avec une base
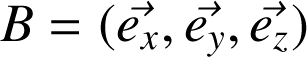fixe, les composantes de la dérivée du vecteur
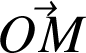sont les dérivées des composantes du vecteur :
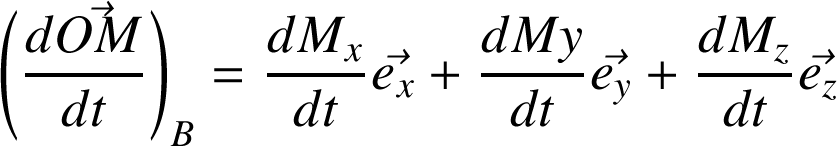
Cas particulier : dérivée d'un vecteur
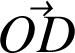de norme constante
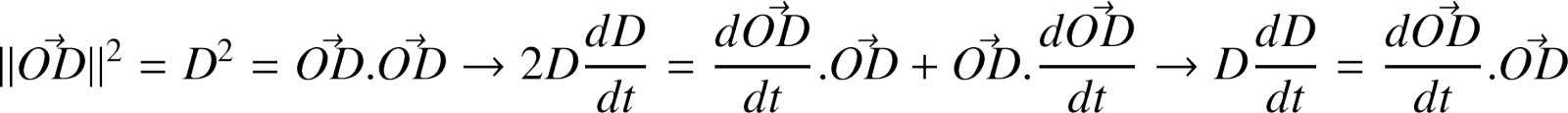
Si D = cste,
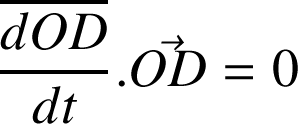
Le vecteur dérivée est normal au vecteur : c'est notamment le cas pour des vecteurs unitaires fixes.
Définition :
Dans une base
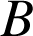mobile par rapport au référentiel
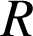de l'observateur :
