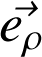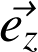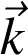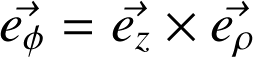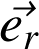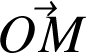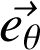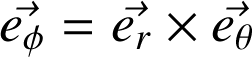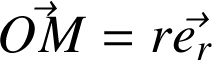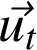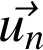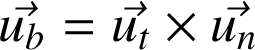Ces bases sont formées de vecteurs unitaires orthonormés dont la direction change avec M. Ces vecteurs seront soit placés en O soit rapportés en M (voir schémas).
Définition :
Base locale des coordonnées cylindriques :
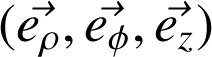
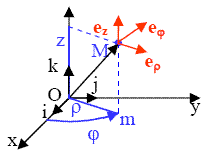 Base locale des coordonnées cylindriques |
|
Relations importantes :
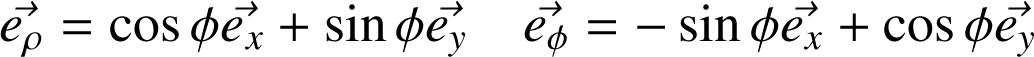
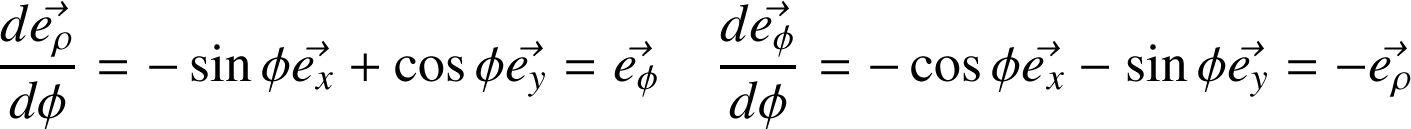
Différentielle :
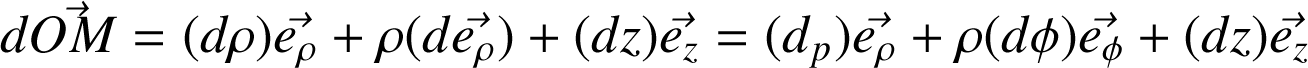
Géométriquement on obtient le même résultat. Dans la base liée à
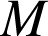 , pour aller de
, pour aller de
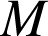 à
à
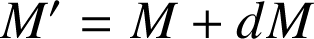 : on va de
: on va de
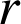 à
à
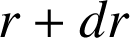 ; on va de
; on va de
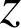 à
à
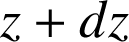 ; on tourne d'un arc de cercle
; on tourne d'un arc de cercle
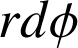 .
.
Définition :
Base locale des coordonnées polaires :
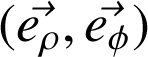 . Espace oxy à deux dimensions.
. Espace oxy à deux dimensions.
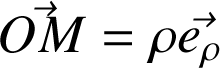
Les relations entre les vecteurs unitaires et leurs dérivées sont inchangées.
Différentielle :
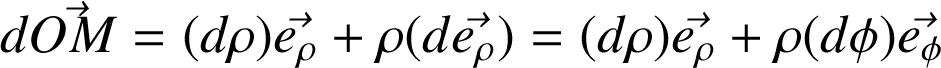
Définition :
Base locale des coordonnées sphériques :
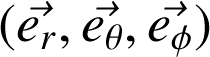
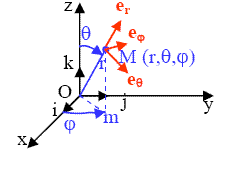 Base locale des coordonnées sphériques |
|
Différentielle :
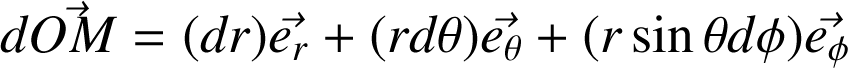
En effet, dans la base liée à
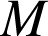 , pour aller de
, pour aller de
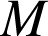 à
à
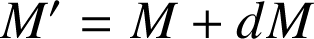 : on va de
: on va de
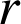 à
à
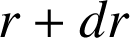 ; on tourne d'un arc de cercle
; on tourne d'un arc de cercle
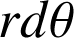 et d'un arc de cercle
et d'un arc de cercle
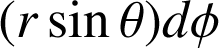 .
.
Définition :
Base de Serret-Frenet des coordonnées intrinsèques :
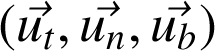
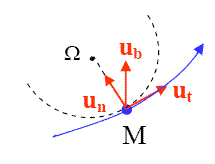 Base de Serret-Frenet des coordonnées intrinsèques | C'est une base locale de vecteurs unitaires rapportée en M. Elle est formée du vecteur ut tangent à la courbe, du vecteur dérivée normal à
|
Définition :
On définit le rayon de courbure Rc de la courbe en M : c'est le rayon ΩM du cercle intérieur, de centre Ω, qui est tangent à la trajectoire au point M. La grandeur 1/Rc est appelée courbure. Le point Ω est appelé centre de courbure (en M) de la courbe. Il satisfait la relation :
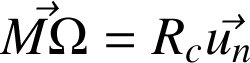
Cas particulier : si la trajectoire du point M est un cercle de centre O et de rayon R, alors Ω = O et Rc = R.