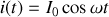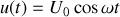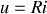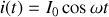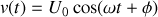Puissance moyenne dissipée par une résistance, notion de valeur efficace
Explication :
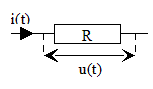 . | La résistance
Posons
|
Rappel :
Par définition, vue dans le chapitre 2, la puissance reçue par la résistance est
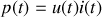. Cette expression donne une valeur instantanée (c'est à dire à l'instant
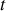) de la puissance consommée par
.
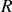On peut facilement écrire
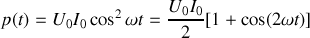. Cette expression montre que
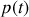, qui s'annule toutes les demi périodes et qui passe par le maximum
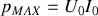, possède une valeur moyenne notée
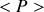et égale bien sûr à
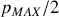, puisque la valeur moyenne sur une période du cosinus est nulle.
Définition :
Appelons
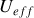et
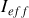respectivement la tension continue aux bornes de
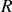et l'intensité continue qui la traverse, telles que la puissance consommée par
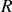soit égale à
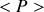, on obtient
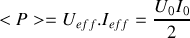, soit
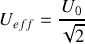et
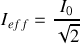
Définition :
Les quantités
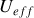et
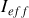s'appellent respectivement tension efficace et intensité efficace associées à
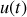et
.
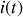Remarque :
La puissance instantanée
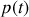consommée dans une résistance
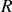et l'énergie
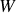consommée pendant une période
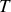sont reliées par les relations
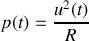, soit
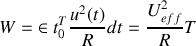, ce qui fournit une relation utile :
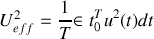
Puissance moyenne reçue par un dipôle
Méthode :
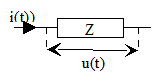 . | Soit maintenant le dipôle ci-contre, d'impédance
|
En développant le produit des cosinus selon une relation classique, on obtient
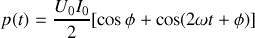. Comme précédemment, cette quantité est une expression instantanée, et il lui correspond la valeur moyenne
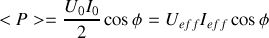
Définition : Notation complexe de p(t)
En notation complexe
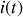et
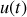s'écrivent respectivement
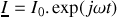et
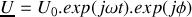. Si l'on note
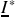le complexe conjugué de
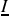, on voit qu'on peut définir une quantité complexe
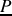par
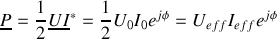, dont on tire
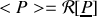, où
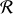désigne la partie réelle de
.
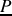Puissance moyenne pour quelques dipôles élémentaires
Résistance
:
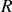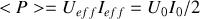.Inductance
:
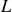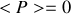, car le complexe
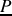est purement imaginaire (on a déjà vu que
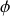vaut
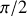).Capacité
:
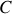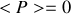, même raison que pour la self (on a déjà vu que
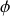vaut
).
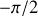Remarque :
Ainsi, la bobine et le condensateur ne dissipent-ils aucune puissance : pendant une demi période ils fonctionnent en générateur, pendant l'autre moitié ils fonctionnent en récepteur : ils ne stockent donc aucune énergie.
Méthode : Dipôle quelconque
Soit un dipôle dont l'impédance s'écrit
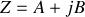, où encore d'admittance
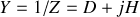. Si
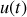et
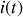sont la tension à ses bornes et l'intensité du courant qui le traverse, la loi d'Ohm appliquée à ce dipôle s'écrit, en notation complexe,
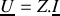, ou encore
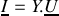, soit
.
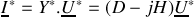La puissance complexe vue ci-dessus s'écrit
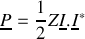, ou encore
.
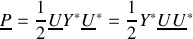Or, le produit d'un nombre complexe par son complexe conjugué est un nombre réel égal au carré de son module : donc
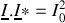, et
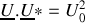. D'où les relations importantes :
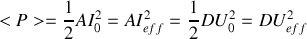
Remarque :
Ces expressions montrent que, puisque
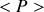est une quantité positive, les parties réelles
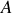de l'impédance
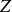et
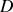de l'admittance
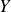doivent être toujours positives.
Définition :
La partie réelle de
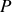s'appelle puissance active, sa partie imaginaire puissance réactive. Le terme
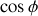s'appelle facteur de puissance. Il doit bien sûr être le plus voisin possible de l'unité.
Remarque sur le comportement de la bobine et du condensateur
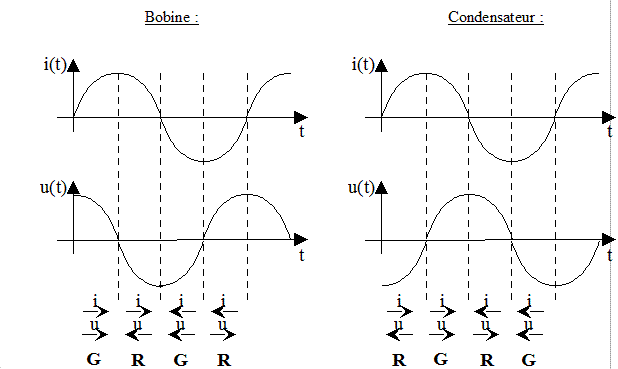
Remarque :
Pendant deux quarts de période, la bobine et le condensateur se comportent comme des générateurs et fournissent de l'énergie au circuit. Pendant les deux autres quarts, ils se comportent comme des récepteurs et emmagasinent de l'énergie. Leur puissance moyenne sur une période est donc bien nulle.
