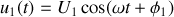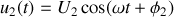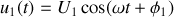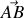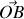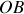Fondamental :
Nous allons voir ici pourquoi la notation complexe est indispensable pour additionner et pour faire le quotient de deux fonctions sinusoïdales, et comment il faut s'y prendre pour cela. Remarquons que la notation complexe qui va être introduite ici est très générale, car elle est liée uniquement à l'existence des fonctions sinusoïdales ; vous pouvez donc la rencontrer aussi en mécanique (mouvements vibratoires) et en optique (interférences, diffraction, holographie...).
Remarque :
Par convention usuellement adoptée, on désignera par la lettre minuscule
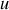 la fonction du temps
la fonction du temps
 , et par une majuscule (
, et par une majuscule (
 , etc...) l'amplitude constante de cette fonction.
, etc...) l'amplitude constante de cette fonction.
Addition de deux grandeurs sinusoïdales
 circuit série | Soient deux éléments de circuit placés en série, aux bornes desquels existent respectivement les tensions
|
La tension existant entre A et C étant nécessairement sinusoïdale à la même fréquence, on la note
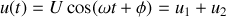 , et le problème est alors de calculer
, et le problème est alors de calculer
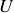 et
et
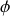 en fonction de
en fonction de
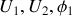 et
et
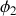 . Il existe pour cela trois méthodes :
. Il existe pour cela trois méthodes :
Addition directe par méthode algébrique
En décomposant les trois cosinus avec des relations classiques, on obtient :
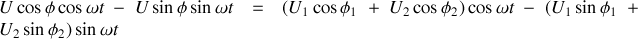 .
.
L'égalité devant être vérifiée à chaque instant, on doit donc avoir
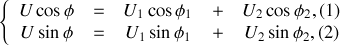
Ces deux relations permettent de calculer
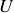 et
et
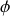 . Inutile d'en dire plus: vous voyez que cette méthode, déjà peu pratique lorsqu'on additionne deux tensions ou deux courants, devient inutilisable lorsqu'il y en a plus. On lui préfère donc les deux méthodes suivantes :
. Inutile d'en dire plus: vous voyez que cette méthode, déjà peu pratique lorsqu'on additionne deux tensions ou deux courants, devient inutilisable lorsqu'il y en a plus. On lui préfère donc les deux méthodes suivantes :
Méthode graphique : représentation de Fresnel
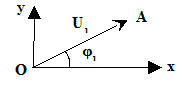 . | Elle consiste à remplacer une fonction sinusoïdale par un vecteur, comme ci-contre pour
|
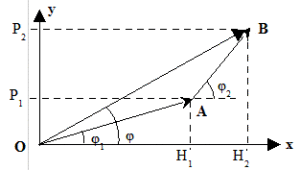 . | La figure ci-contre montre l'addition des tensions
|
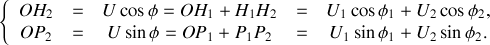
Les relations qui lient
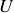 et
et
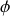 à
à
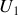 ,
,
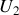 ,
,
 et
et
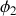 sont les mêmes que celles établies dans la méthode directe : le vecteur
sont les mêmes que celles établies dans la méthode directe : le vecteur
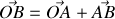 est donc l'image géométrique de la tension
est donc l'image géométrique de la tension
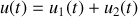 .
.
Méthode des nombres complexes
Rappel :
Rappelons d'abord les différentes expressions d'un nombre complexe :
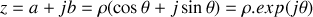 , soit
, soit
 et
et
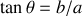 .
.
Dans ces expressions,
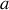 et
et
 sont les parties réelle et imaginaire de
sont les parties réelle et imaginaire de
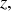
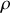 son module et
son module et
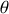 son argument.
son argument.
Le complexe conjugué de
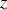 est
est
 , ce qui fournit les relations simples :
, ce qui fournit les relations simples :
 .
.
On a donc
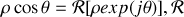 désignant la partie réelle du nombre complexe entre crochets.
désignant la partie réelle du nombre complexe entre crochets.
Méthode :
La méthode consiste à remplacer la fonction sinusoïdale par le nombre complexe correspondant, mais sans le restreindre à sa partie réelle. Ainsi les trois tensions
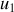 ,
,
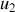 et
et
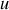 se représentent respectivement par
se représentent respectivement par
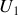 ,
,
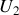 et
et
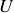 , où la barre _ rappelle qu'il s'agit de quantités complexes dépendant du temps :
, où la barre _ rappelle qu'il s'agit de quantités complexes dépendant du temps :
 .
.
La somme
 revient alors à résoudre l'équation complexe
revient alors à résoudre l'équation complexe
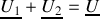 , soit
, soit
 .
.
En égalant les parties réelle et imaginaire de cette égalité complexe, on retrouve facilement les deux expressions déjà obtenues pour calculer
 et
et
 :
:
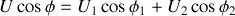 et
et
 .
.
La somme des deux tensions
 et
et
 se traite donc bien en faisant la somme des images complexes
se traite donc bien en faisant la somme des images complexes
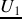 et
et
 correspondantes.
correspondantes.
Remarque : importante
Lorsqu'on écrit
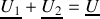 , le terme
, le terme
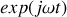 , présent partout, s'élimine tout seul. Il en sera de même dans toutes les équations qui seront écrites en utilisant la notation complexe. Ce terme peut donc, éventuellement, être systématiquement omis.
, présent partout, s'élimine tout seul. Il en sera de même dans toutes les équations qui seront écrites en utilisant la notation complexe. Ce terme peut donc, éventuellement, être systématiquement omis.
L'avantage de la notation complexe sur les deux autres méthodes apparaît lorsqu'on doit faire le quotient d'une tension par un courant en régime sinusoïdal :
Quotient de deux grandeurs sinusoïdales : notion d'impédance complexe
Explication :
En régime permanent continu, si une différence de potentiel
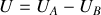 existe entre A et B, un courant d'intensité
existe entre A et B, un courant d'intensité
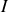 circule de A vers B et le quotient
circule de A vers B et le quotient
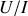 traduit la résistance
traduit la résistance
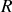 du circuit entre A et B. Cette résistance
du circuit entre A et B. Cette résistance
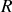 est évidemment constante.
est évidemment constante.
Supposons que cet élément soit alimenté en régime permanent sinusoïdal: la différence de potentiel entre
 et
et
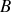 s'écrit alors
s'écrit alors
 et le courant circulant dans l'élément est
et le courant circulant dans l'élément est
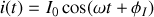 , où dans le cas général
, où dans le cas général
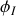 est différent de
est différent de
 . Le quotient des valeurs instantanées est alors
. Le quotient des valeurs instantanées est alors
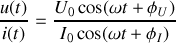
Attention :
Or, les deux cosinus varient entre -1 et +1 en passant par zéro à des instants différents en raison de la différence entre
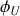 et
et
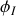 . Le rapport
. Le rapport
 prend donc toutes les valeurs entre
prend donc toutes les valeurs entre
 et
et
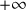 ! Avec les fonctions du temps
! Avec les fonctions du temps
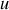 et
et
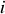 , il est donc impossible de retrouver la notion de résistance du circuit.
, il est donc impossible de retrouver la notion de résistance du circuit.
Méthode :
Le passage à la notation complexe permet de résoudre cette difficulté. En effet, le rapport
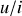 s'écrit alors :
s'écrit alors :
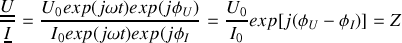
Définition :
Comme précédemment, le terme
 s'est simplifié. Le nombre complexe
s'est simplifié. Le nombre complexe
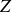 , indépendant du temps, s'appelle impédance complexe, ou simplement impédance, de l'élément de circuit étudié. L'impédance se mesure en Ohm, comme les résistances. La barre inférieure n'y figure pas, car cette notation est réservée à la transposition complexe d'une fonction du temps.
, indépendant du temps, s'appelle impédance complexe, ou simplement impédance, de l'élément de circuit étudié. L'impédance se mesure en Ohm, comme les résistances. La barre inférieure n'y figure pas, car cette notation est réservée à la transposition complexe d'une fonction du temps.
Méthode :
Avec cette notation, on peut écrire
 , relation qui traduit la loi d'Ohm en régime sinusoïdal. Ainsi, toutes les méthodes de résolution de circuits vues en régime continu (diviseur de tension, lois de Kirchhoff, théorème de Thévenin, etc...) sont encore applicables en régime sinusoïdal, à condition de travailler avec les impédances complexes. Seule la notation complexe permet cette transposition, ce qui justifie son importance.
, relation qui traduit la loi d'Ohm en régime sinusoïdal. Ainsi, toutes les méthodes de résolution de circuits vues en régime continu (diviseur de tension, lois de Kirchhoff, théorème de Thévenin, etc...) sont encore applicables en régime sinusoïdal, à condition de travailler avec les impédances complexes. Seule la notation complexe permet cette transposition, ce qui justifie son importance.
Les impédances se traitent comme des résistances: en série elles s'ajoutent, en parallèle ce sont leurs inverses qui s'ajoutent (l'inverse
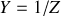 de l'impédance s'appelle admittance complexe).
de l'impédance s'appelle admittance complexe).
Remarque :
Lorsque vous connaissez l'impédance complexe qui existe entre deux points d'un circuit, vous êtes en possession de deux informations capitales :
Le module de
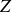 donne le rapport
donne le rapport
 des amplitudes de la tension
des amplitudes de la tension
 appliquée à un dipôle au courant
appliquée à un dipôle au courant
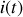 qui le traverse.
qui le traverse.L'argument de
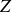 donne la différence de phase
donne la différence de phase
 , c'est-à-dire le déphasage de la tension
, c'est-à-dire le déphasage de la tension
 sur le courant
sur le courant
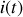 .
.
Quelques impédances élémentaires
Résistance
Remarque :
C'est le seul cas pour lequel la loi d'Ohm est vérifiée en valeur instantanée. On peut écrire en effet
 , soit
, soit
 : l'impédance est donc égale à
: l'impédance est donc égale à
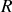 , elle est réelle : une résistance n'introduit pas de déphasage entre tension et courant.
, elle est réelle : une résistance n'introduit pas de déphasage entre tension et courant.
Capacité
Explication :
L'intensité
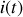 qui traverse un condensateur
qui traverse un condensateur
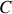 , la tension
, la tension
 à ses bornes et la charge
à ses bornes et la charge
 qu'il porte sont liées par les relations
qu'il porte sont liées par les relations
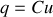 et
et
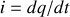 , soit
, soit
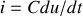
Si la tension s'écrit
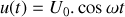 , on obtient alors
, on obtient alors
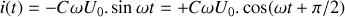 .
.
En notation complexe, ceci s'écrit
 , soit
, soit
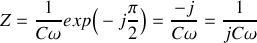
Remarque :
On en déduit donc la relation entre les amplitudes du courant et de la tension :
 . De plus, l'argument de
. De plus, l'argument de
 est
est
 , donc la tension
, donc la tension
 est en retard sur le courant
est en retard sur le courant
 . On peut aussi écrire :
. On peut aussi écrire :
 , avec ici
, avec ici
 , ce qui redonne
, ce qui redonne
 : dans un condensateur, le courant est en quadrature avance sur la tension à ses bornes.
: dans un condensateur, le courant est en quadrature avance sur la tension à ses bornes.
Inductance
Explication :
L'intensité
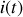 qui traverse un bobinage d'inductance
qui traverse un bobinage d'inductance
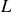 et la tension
et la tension
 à ses bornes sont liées par la relation :
à ses bornes sont liées par la relation :
 .
.
Si l'on écrit le courant comme
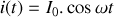 , on obtient
, on obtient
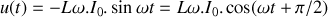 .
.
En notation complexe :
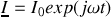 ,
,
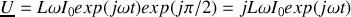 , soit
, soit
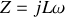
Remarque :
D'où la relation entre les amplitudes du courant et de la tension :
 .
.
L'argument de
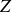 est
est
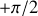 , donc la tension aux bornes d'une inductance est en quadrature avance sur le courant qui la traverse.
, donc la tension aux bornes d'une inductance est en quadrature avance sur le courant qui la traverse.
En résumé
Passage de
 et
et
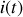 à la représentation complexe :
à la représentation complexe :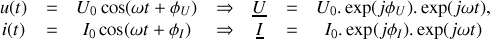
Loi d'Ohm en RPS :
 ou
ou
 ,
,
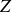 et
et
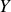 étant respectivement l'impédance et l'admittance d'une branche du circuit aux bornes de laquelle la différence de potentiel est
étant respectivement l'impédance et l'admittance d'une branche du circuit aux bornes de laquelle la différence de potentiel est
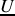 .
.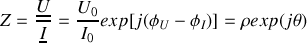 fournit deux informations :
fournit deux informations : le module
le module
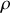 de
de
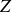 donne le rapport des amplitudes
donne le rapport des amplitudes
 : comme pour les circuits en RPC, l'une de ces 2 grandeurs (souvent c'est
: comme pour les circuits en RPC, l'une de ces 2 grandeurs (souvent c'est
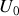 ) est connue ou facilement calculable : l'autre s'en déduit donc facilement. Le module de
) est connue ou facilement calculable : l'autre s'en déduit donc facilement. Le module de
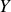 donne évidemment l'inverse de ce rapport.
donne évidemment l'inverse de ce rapport. L'argument
L'argument
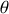 de
de
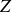 donne le déphasage
donne le déphasage
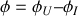 de la tension
de la tension
 sur le courant
sur le courant
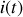 ; celui de
; celui de
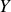 donne
donne
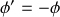 .
.Retour à la notation réelle pour un courant ou une tension :

Pour les dipôles élémentaires :
Remarque sur les termes de phase, piège à éviter
Remarque :
Dans beaucoup d'exercices les phases
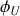 ou
ou
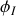 ne sont pas données. Les phases sont comme les altitudes, elles sont arbitraires et n'ont de sens que lorsqu'on leur a fixé une origine. C'est le déphasage qui, comme la hauteur séparant deux points, est important. Vous devez donc, si elle n'est pas imposée, choisir une origine pour le calcul des déphasages.
ne sont pas données. Les phases sont comme les altitudes, elles sont arbitraires et n'ont de sens que lorsqu'on leur a fixé une origine. C'est le déphasage qui, comme la hauteur séparant deux points, est important. Vous devez donc, si elle n'est pas imposée, choisir une origine pour le calcul des déphasages.
On peut choisir l'origine des phases sur le courant :
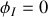 ,
,
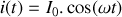 . Dans ce cas l'argument
. Dans ce cas l'argument
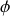 de
de
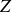 donne directement
donne directement
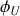 . Mais on peut aussi prendre cette origine sur la tension d'alimentation
. Mais on peut aussi prendre cette origine sur la tension d'alimentation
 :
:
 ,
,
 : dans ce cas l'argument
: dans ce cas l'argument
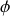 de
de
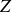 donne
donne
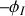 .
.
Attention : au piège
Ne pas revenir trop vite à la notation réelle : lorsqu'on a
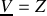 .
.
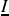 avec
avec
 , l'erreur souvent rencontrée est d'écrire
, l'erreur souvent rencontrée est d'écrire
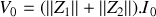 ; le module d'une somme n'est pas égal à la somme des modules... Vous devez garder la notation complexe jusqu'au bout des calculs.
; le module d'une somme n'est pas égal à la somme des modules... Vous devez garder la notation complexe jusqu'au bout des calculs.