Rappels et définitions
Rappel :
Régime permanent continu (RPC) : les sources d'alimentation (en tension ou en courant) sont constantes au cours du temps. Toutes les tensions et les intensités existant dans le circuit sont donc elles aussi indépendantes du temps.
Définition :
Régime transitoire : il apparaît lorsque, à un instant donné, les sources d'alimentation varient au cours du temps. Cette variation peut être brutale (échelon) ou progressive (rampe linéaire ou autre). Vous verrez dans le chapitre VI que le régime transitoire disparaît toujours (plus ou moins vite), et que lorsqu'il a disparu le circuit fonctionne dans un nouveau régime dont la dépendance au cours du temps est analogue à celle des sources d'alimentation (continu si échelon, linéaire si rampe, etc...).
Définition :
Régime permanent sinusoïdal (RPS) : c'est l'état électrique d'un circuit alimenté par une source de tension ou de courant sinusoïdale, lorsque le régime transitoire a disparu. Les tensions et les courants existant en tous points du circuit sont alors aussi sinusoïdales, avec la même période que celle de la source. Ainsi, si le circuit est alimenté par un générateur délivrant une tension
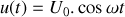, un courant
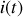circulant dans une branche du circuit s'écrira
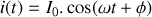, où
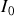est l'amplitude de
,
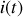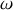la pulsation liée à la fréquence F par
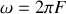, et
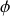le déphasage de
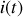par rapport à
.
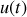Le but de ce chapitre est de présenter les méthodes permettant de déterminer l'amplitude
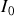et le terme de phase
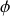de ce courant ; puis, à titre d'exemple, nous ferons l'étude détaillée d'un circuit particulier : association d'une capacité, d'une inductance et d'une résistance placées en série. Les problèmes énergétiques (puissance en régime sinusoïdal) seront abordés en fin de chapitre.
Stratégie
Méthode :
Dans l'étude d'un circuit en RPC, à partir de la somme des courants (loi des nœuds) et des tensions (loi des mailles), ainsi que du rapport
(loi d'Ohm), on a établi diverses méthodes de résolution (Kirchhoff, superposition, Thévenin, Norton etc...). Si l'on parvient à réaliser ces deux opérations (somme et quotient) avec des grandeurs sinusoïdales, toutes les méthodes vues en RPC pourront alors être utilisées ici et l'étude des RPS sera quasiment achevée. D'où l'importance du
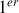paragraphe.
