i) Additivité.

Soient un champ vectoriel 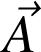et un potentiel scalaire 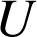associés à une masse 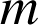ou à une charge électrique 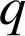. Pour un ensemble de masses ou de charges,

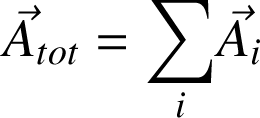
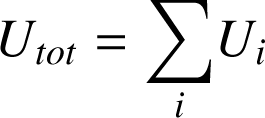
ii) 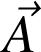est perpendiculaire à la surface équipotentielle, en .

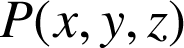Cette propriété est vraie uniquement pour les champ associé à des forces conservatives pour lesquelles on peut définir une fonction potentiel. Démonstration : on calcule la circulation de 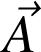pour un déplacement 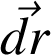du point 1 au point 2 le long de l'équipotentielle ,

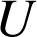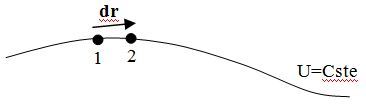
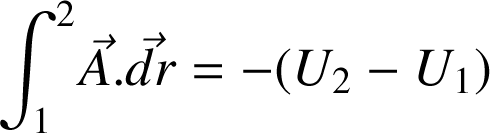
Le second membre de l'équation est toujours nul car on se déplace sur l'équipotentielle. On en déduit la propriété : .

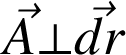iii) 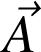est orienté vers les potentiels décroissants.

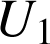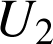Cette propriété est vraie uniquement pour les champ associé à des forces conservatives pour lesquelles on peut définir une fonction potentiel. Démonstration : soit deux équipotentielles et telles que 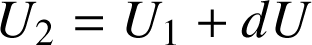. Ces équipotentielles sont séparées dans une région de l'espace par une distance .

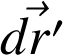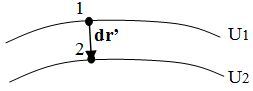
On sait que 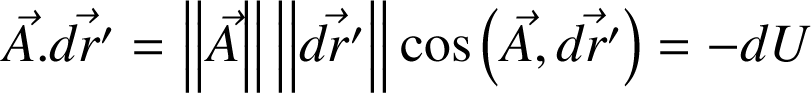. L'angle formé par les deux vecteurs ne peut prendre que deux valeurs : 0° et 180° (propriété ii). Si 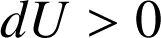, alors l'angle vaut 180° et 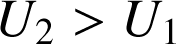. Dans le cas contraire, , l'angle vaut 0° et 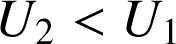. La conclusion pour les deux cas est que le vecteur champ est toujours orienté vers les potentiels décroissants.

iv) Propriétés de symétrie.

Ce sont des propriétés importantes pour les champs (simplification des calculs), c'est au programme des cours de physique du S3.