De façon très générale, on dit qu'un champ est une grandeur qui est définie en chaque point
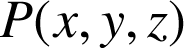de l'espace. On va distinguer les champs vectoriel et scalaire :
Champ vectoriel
Définition :
Ensemble de vecteurs
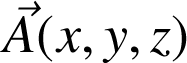où chaque vecteur est associé à un point
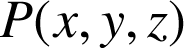de l'espace. Le point d'application de
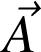est en
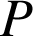, et ce vecteur est caractérisé par une norme et un sens, que l'on obtient à partir des coordonnées de ce vecteur,
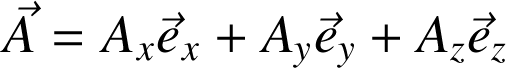
Exemple :
champ de vitesses (écoulement de fluide)
Définition : Ligne de champ
Courbe reliant tous les points
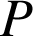pour lesquels
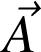est tangent à cette courbe. Les deux schémas ci-dessous illustrent en traits pointillés une ligne de champ (ii) et une courbe reliant des points
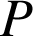qui n'est pas une ligne de champ (i). Souvent la ligne de champ est tracée avec une flèche (sens) qui indique le sens des vecteurs champs tangents à la ligne de champ.
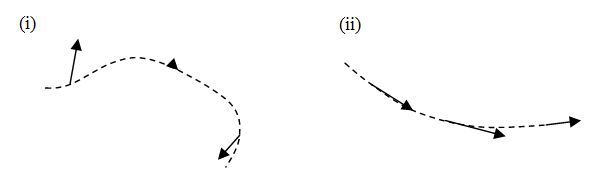
Champ scalaire
Définition :
Ensemble de nombres
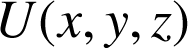où chaque nombre est associé à un point
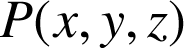de l'espace.
Exemple :
Champ de température, de pression, d'altitude (météo)
Définition : Courbe ou surface équipotentielle
Courbe ou surface à trois dimensions sur les points de laquelle
.
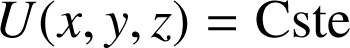