On s'intéresse ici au cas particulier des champs newtoniens. Ce sont les champs vectoriels et scalaires associés aux forces newtoniennes (dépendance en l'inverse du carré de la distance) et aux potentiels associés, respectivement.

i) Champ gravitationnel 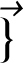et potentiel gravitationnel .

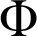Le champ vectoriel 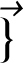créé par la masse 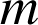et associé à la force gravitationnelle est défini par l'équation :

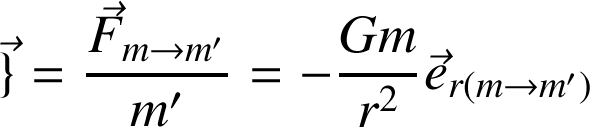
La masse 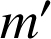est celle de la particule test 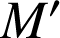, elle est ignorée par la suite. Le champ gravitationnel s'exprime en 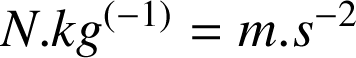, il a la dimension d'une accélération.

Le potentiel 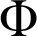associé à 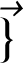est un champ scalaire, défini par la relation :

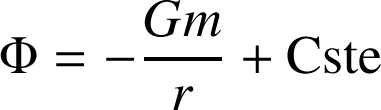
Il s'exprime en .

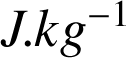Le schéma suivant présente les vecteurs champs gravitationnels associés à quelques points de l'espace.

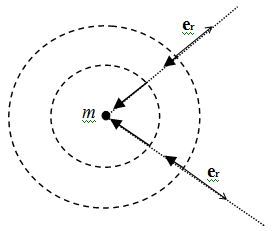
En chaque point, on peut associer une valeur précise du potentiel. Les droites en traits pointillés représentent les lignes de champs, tangentes aux vecteurs champs, et les cercles en traits pointillés sont des équipotentielles, reliant entre eux les points ayant même potentiel (il s'agit des points situés à une même distance de 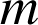). Dans un espace à trois dimensions, chaque rayon d'une sphère centrée en 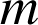est une ligne de champ (les lignes de champ sont radiales). Ces lignes de champ sont orientées vers 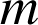. Chaque surface de sphère de rayon 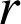centrée en 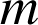représente une équipotentielle. A la surface de la Terre, .

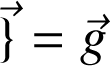ii) Champ électrostatique 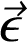et potentiel électrostatique .

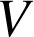Le champ vectoriel 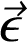créé par la charge q et associé à la force de Coulomb est défini par l'équation :

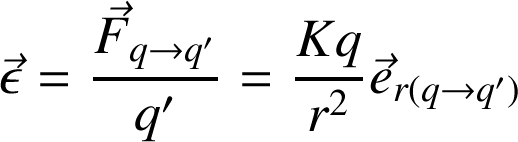
La charge 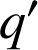est celle de la particule test 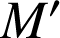, elle est ignorée par la suite. Le champ électrostatique s'exprime en 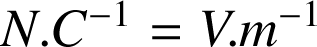(volt par mètre).

Le potentiel 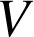associé à 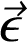est un champ scalaire, défini par la relation :

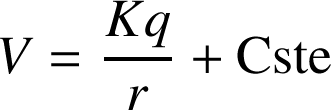
Il s'exprime en 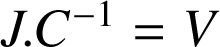(volt).

Les schémas suivants présentent les vecteurs champs électrostatiques associés à quelques points de l'espace, pour une charge 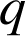de signe positif ou négatif.

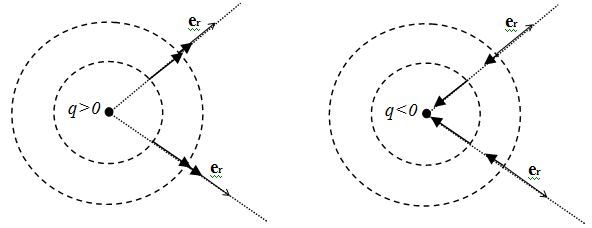
En chaque point, on peut associer une valeur précise du potentiel. Les traits en pointillés représentent les lignes de champs, tangentes aux vecteurs champs, ainsi que les équipotentielles, reliant entre eux les points ayant même potentiel (il s'agit des points situés à une même distance de 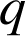). Dans un espace à trois dimensions, chaque rayon d'une sphère centrée en 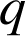est une ligne de champ. Ces lignes de champ sont orientées vers 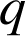lorsque la charge est négative, et s'en éloignent lorsque la charge est positive. Chaque surface de sphère de rayon 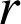centrée en 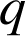représente une équipotentielle.