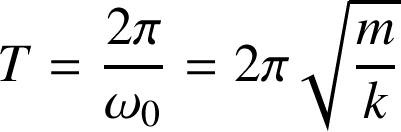Méthode : Chute d'un corps avec frottement.
Un skieur S commence à dévaler une pente de 30°. Sachant que
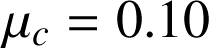, déterminer i) son accélération, ii) sa vitesse après 6s.
La démarche à suivre pour résoudre ce type de problème est la suivante. i) Faire un schéma. ii) Choisir un référentiel (par exemple oxy) galiléen. iii) Indiquer les forces appliquées à S. iv) Appliquer le PFD, projeter sur les axes.
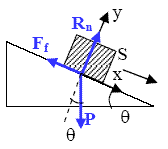
Les forces appliquées à S sont les suivantes :
Le poids :
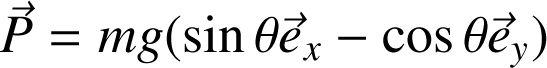
La réaction du support :
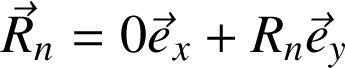
La force de frottement :
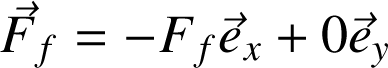
L'application du PFD fournit deux relations :
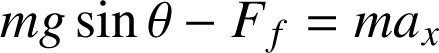
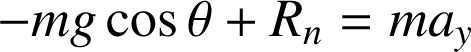
auxquelles vient s'ajouter :
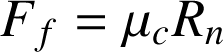
Comme le mouvement est orienté selon ox,
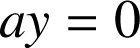. On obtient :
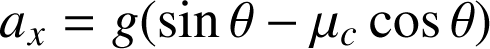
et par intégration,
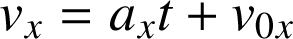
On peut remarquer que si la vitesse initiale est nulle,
. Il ne reste plus qu'à faire l'application numérique. Le coefficient de frottement statique
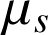est obtenu en exprimant la condition d'équilibre dans l'expression de
:
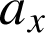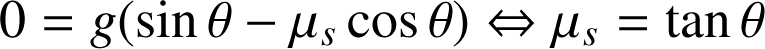
Fondamental : Oscillateurs harmoniques
Un oscillateur harmonique à une dimension est un système dont le degré de liberté, par exemple
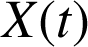, varie au cours du temps selon une loi sinusoïdale,
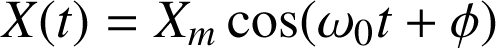
Les constantes
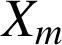(amplitude) et
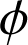(phase) sont définies en t=0 par les conditions initiales
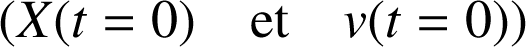. La pulsation (supposée constante) est reliée à la période
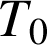(un aller-retour) du mouvement d'oscillation par la relation :
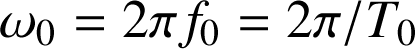
En dynamique, on obtient d'abord l'équation du mouvement, puis sa solution
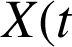). L'équation du mouvement d'un oscillateur harmonique, obtenue par application du PFD ou d'un théorème de conservation, peut toujours se ramener, par un changement de variable approprié, à une équation différentielle caractéristique (appelée équation canonique) du type :
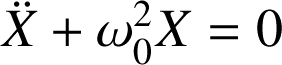
dont on peut vérifier que l'expression de
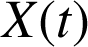est une solution (voir aussi cours de mathématique). A titre d'exemple on peut citer le pendule décrit par la variable
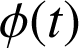, le ressort décrit par la variable x(t) ou y(t), à la limite des petites oscillations, comme nous allons le voir ci-dessous.
Exemple :
Pendule simple
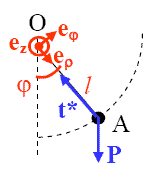
Le point O est un point fixe. Un pendule de longueur
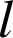décrit un mouvement circulaire autour de O. Le mouvement d'oscillation se fera autour de la verticale et peut être décrite par la variable
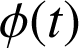. La cinématique nous dit que (section 3.4, mouvement circulaire non-uniforme) :
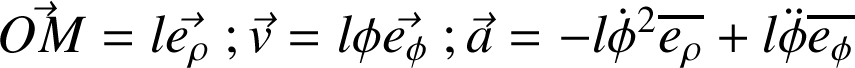
Dans le référentiel (R) terrestre supposé galiléen, on travaille avec une base locale. Soit
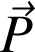le poids du point matériel A et
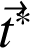la tension qu'exerce le fil sur A. Appliquons le PFD :
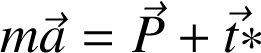
Selon
:
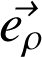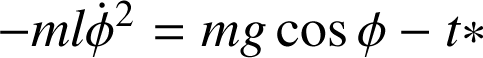
Selon
:
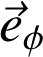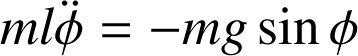
Cette dernière équation se ré-écrit :
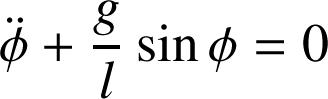
Aux petits angles
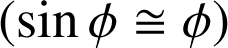, on retrouve une équation similaire à l'équation canonique de l'oscillateur harmonique :
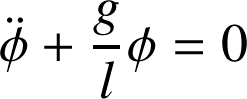
La période T vaut :
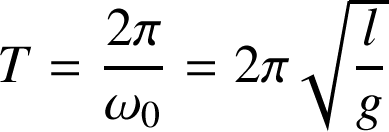
Définition :
Un ressort est un système déformable qui tend à retourner à sa position d'équilibre, située en O, avec une force de rappel (loi de Hooke,
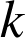> 0 ):
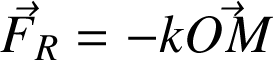
Exemple :
Considérons le cas d'un ressort horizontal. On peut écrire (voir figure) :
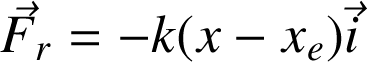
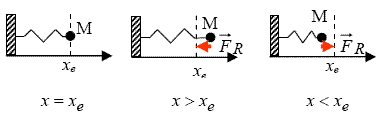
Souvent, on choisit
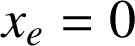comme origine. Un problème fréquemment traité est celui où le point matériel M est posé sur un support :
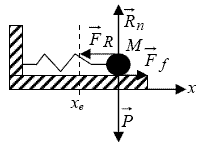
Si on effectue un bilan de forces, on va considérer selon la direction verticale le poids
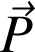de
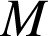et la réaction
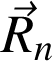du support, et selon la direction horizontale, la force de rappel
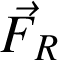du ressort, et la force de frottement
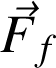. Si on néglige cette dernière, l'équation du mouvement s'obtient par application du PFD selon ox :
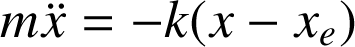
On effectue alors un changement de variable
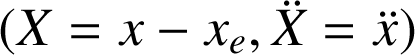pour se ramener à l'équation canonique de l'oscillateur harmonique :
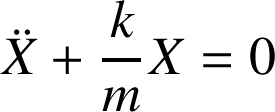
La période T du ressort horizontal vaut :
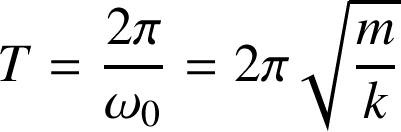
Exemple :
Pour un ressort vertical (voir figure), prenons comme position d'équilibre celle associée au ressort sans masse :
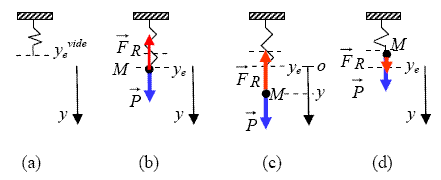
Si on accroche une masse m, le ressort s'allonge. Considérons la situation d'équilibre du point matériel M (Fig. b). Le PFD s'écrit :
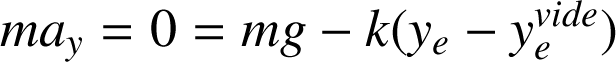
On obtient l'allongement du ressort :
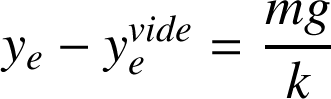
Lorsque la masse
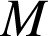et le ressort sont en mouvement, l'oscillation s'effectue autour de
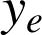(Fig. c et d). Prenons le cas (c). L'allongement de l'ensemble vaut
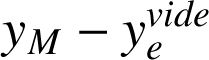. Si y est compté par rapport à
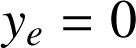l'allongement est égal à
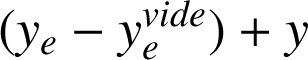. L'application du PFD au point
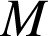donne :
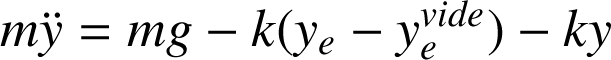
En utilisant la relation qui exprime l'allongement du ressort, on obtient l'équation canonique :
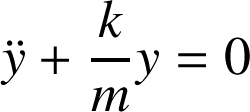
La période T du ressort vertical vaut :
