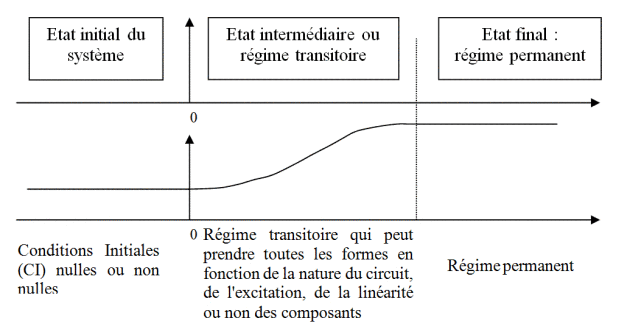
Définition :
Un régime transitoire est un régime électrique qui s'instaure lorsqu'un circuit électrique passe d'un régime permanent à un autre: tension et courant évoluent dans le temps à partir de valeurs initiales adoptées à la fin du premier régime (instant initial
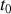le plus souvent pris égal à 0), jusqu'à retrouver des valeurs correspondant au second régime. Sa durée est limitée et on peut définir des constantes de temps, appelées
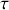, caractéristiques des dipôles présents dans le circuit. La connaissance de ces constantes de temps est essentielle car elles définissent le choix des dipôles à utiliser pour réaliser un circuit dont on veut qu'il ait des propriétés prédéfinies.
Explication :
Méthode :
Les lois des nœuds et des mailles sont applicables aux valeurs instantanées des courants et tensions et permettent de définir des équations différentielles dont la résolution conduit aux expressions des charges, tensions ou courants sous forme de fonctions du temps correspondant à la réponse d'un circuit au changement de régime.
Fondamental :
Puisque les équations recherchées dépendent des dipôles présents dans le circuit, différents cas sont à envisager :
1 - Lorsque le circuit ne contient que des dipôles ohmiques et des condensateurs dont le regroupement aboutit à une résistance équivalente et un condensateur équivalent en série, on doit obtenir une équation différentielle du premier ordre en tension puisque
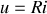et
.
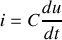Attention :
Important : lors d'une variation brutale de la tension dans un circuit
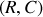, la charge
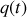du condensateur, et donc la tension
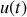à ses bornes, ne peuvent pas varier de façon brutale, donc ne doivent pas présenter de discontinuité.
Explication :
En effet, si c'était le cas la quantité
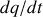serait infinie, et donc le courant chargeant le condensateur aussi ; or ceci est impossible.
A l'instant juste antérieur à l'instant initial, la charge est donc identique à celle existant à l'instant juste postérieur à l'instant initial, ce qui se traduit par
.
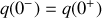Fondamental :
2 - De même, lorsque le circuit ne contient que des dipôles ohmiques et des selfs, après leur regroupement on doit obtenir une équation différentielle du premier ordre en courant puisque
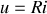et
.
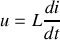Attention :
Important : lors d'une variation brutale de la tension dans un circuit
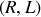, le courant passant dans la self ne peut présenter de discontinuité.
Explication :
Ceci pour la même raison que pour le condensateur : la dérivée
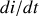ne peut pas être infinie.
Le même raisonnement que pour la charge de la partie précédente conduit donc à
.
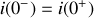Fondamental :
3 - Lorsque le circuit contient à la fois des dipôles ohmiques, des condensateurs et des selfs, on doit obtenir une équation différentielle du second ordre sinon plus.
Définition :
Les deux premiers cas sont alors appelés régimes transitoires du premier ordre, le troisième cas est appelé régime transitoire du second ordre (ou plus).
Nous limiterons notre étude à la réponse d'un circuit contenant un seul générateur délivrant un échelon de tension :
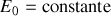, ou une rampe :
.
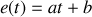Remarque :
Quel que soit le paramètre électrique étudié (courant passant dans une branche, tension à ses bornes, charge d'un condensateur etc...), celui-ci est donné par la résolution d'une équation différentielle de la forme
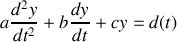
où les coefficients
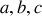dépendent des composants du circuit et donc sont indépendants du temps, et où le second membre
est lié à la source d'alimentation (ici, échelon ou rampe).
Rappel :
La solution de cette équation est une somme de deux termes :
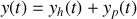, où
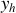est la solution de l'équation sans second membre que l'on appelle « équation homogène » (une ou plusieurs exponentielles décroissantes), et
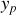une solution particulière de l'équation complète, dont la dépendance temporelle est la même que celle du second membre, qui fait intervenir la source d'alimentation. Comme
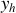disparaît au cours du temps, il est clair que
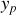représente le régime limite du circuit.
Fondamental :
Il est donc possible de prévoir ce régime limite, sans calcul préalable, simplement en examinant la source d'alimentation : si celle-ci est constante, toutes les variables électriques du circuit tendront vers des constantes ; si celle-ci est une rampe linéaire
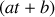, toutes les grandeurs électriques deviendront, une fois le transitoire disparu, des lois linéaires, etc...
