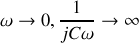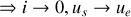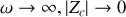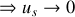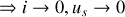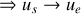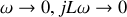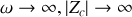Définition :
Lors de l'amplification ou du transfert d'un signal, des tensions parasites, de fréquences différentes, peuvent aussi être amplifiées ou transmises. Un filtre est un quadripôle qui, correctement choisi, permet d'éliminer les signaux parasites en ne laissant passer que le signal utile. On distingue quatre types de filtres :
Filtre passe-bas : les signaux de basses fréquences sont transmis sans atténuation (ou pratiquement sans), les basses fréquences sont éliminées ou fortement réduites.
Filtre passe-haut : cette fois les signaux de hautes fréquences sont transmis sans atténuation, les basses fréquences étant éliminées.
Filtre passe-bande : les signaux transmis ont des fréquences comprises entre
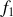et
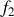, l'intervalle [
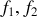] étant appelé bande passante. En dehors de la bande passante, les signaux sont éliminés.Filtre coupe-bande (ou réjecteur de fréquences) : c'est l'opposé du filtre passe-bande ; toutes les fréquences passent, exceptées celles qui sont comprises entre
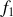et
.
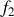L'étude de la réponse en fréquence du filtre est donc indispensable pour le caractériser.
Rappel :
aux fréquences faibles, la bobine est assimilable à un court-circuit tandis que le condensateur est assimilable à un circuit ouvert.
Aux fréquences élevées, la bobine est assimilable à un circuit ouvert alors que le condensateur est assimilable à un court-circuit.
Exemple :
On peut donc déduire très simplement la nature des différents filtres représentés ci-dessous :
 . |
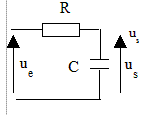Filtre : passe-bas |
 . |
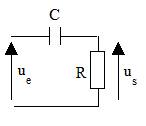Filtre : passe-haut |
 . |
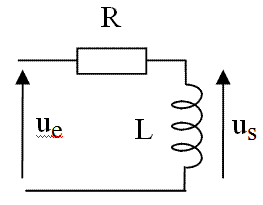Filtre : passe-haut |
 . |
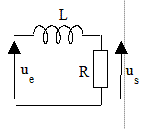Filtre : passe-bas |
Ordre d'un filtre
Complément :
La fonction de transfert complexe peut toujours s'écrire sous la forme d'un rapport de polynômes :
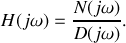
Pour des raisons de stabilité du filtre, le degré du polynôme
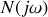est toujours inférieur ou égal au degré du polynôme
.
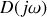On appelle ordre du filtre le degré du polynôme complexe
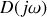selon la variable
.
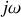Ainsi, le filtre (
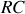) est un filtre passe-bas du
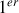ordre.
Pulsation de coupure et bande passante d'un filtre
Soit
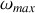la pulsation pour laquelle l'amplification (ou le gain) est maximum. On note
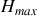(ou
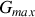) cette valeur. Bien souvent,
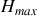vaut 1 et donc
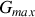vaut 0.
Définition :
On appelle pulsation de coupure la pulsation
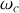telle que
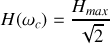
On montre facilement que
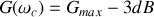
Définition :
La bande passante du filtre est alors l'intervalle de pulsations
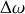, ou de fréquences
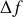, pour lesquelles
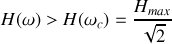, ou
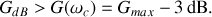
Remarque :
Les filtres du premier ordre dont le dénominateur
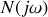est une constante ne présentent qu'une seule pulsation de coupure : ils sont donc passe-haut ou passe-bas. Dans le cas des filtres du second ordre, les deux pulsations de coupure à
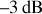ne correspondent pas aux pulsations caractéristiques. Le protocole d'étude de ces filtres est donc différent.
Cas du filtre RC
Exemple :
La fonction de transfert s'écrit
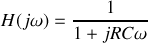; on retrouve la constante de temps
.
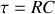En posant
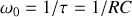, la fonction de transfert devient
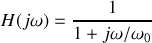. Son module est donnée par
.
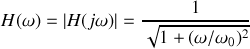Sa valeur maximum est 1, soit un gain de
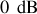pour
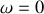, et lorsque
,
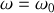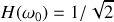, soit un gain de
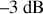, ce qui fait correspondre
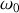avec la pulsation de coupure
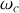(cf. TP n° 5). On a donc aussi
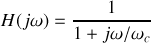et
.
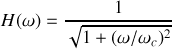L'étude asymptotique de
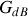montre que :
si
,
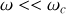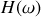reste proche de 1,
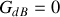, la pente de l'asymptote est nulle.si
,
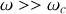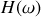est proche de
,
.
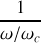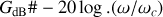Dans ce cas, pour une pulsation
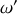égale à
,
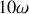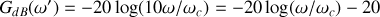; sur une décade, le gain s'atténue de
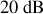, la pente de l'asymptote est donc de
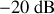par décade.
L'étude asymptotique de
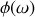montre que :
si
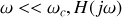étant proche de 1, la partie imaginaire est nulle et la partie réelle positive, donc
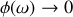.si
,
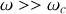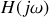étant proche de
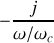, la partie réelle est nulle et la partie imaginaire négative, donc
.
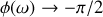